2022年成考高起点每日一练《数学(理)》4月3日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:300
试卷答案:有
试卷介绍: 2022年成考高起点每日一练《数学(理)》4月3日专为备考2022年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 曲线y=2x2+3在点(-1,5)处切线的斜率是
A4
B2
C-2
D-4
-
2. 已知向量
 ,则t=()
,则t=()A-1
B2
C-2
D1
-
3. 已知一次函数y=2x+b的图像经过点(-2,1),则该图像也经过点( )
A(1,7)
B(1,-3)
C(1,5)
D(1,-1)
-
4. 甲、乙各进行一次射击,若甲击中目标的概率是0.4,乙击中目标的概率是0.5,且甲、乙是否击中目标相互独立,则甲、乙都击中目标的概率是()。
A0.9
B0.5
C0.4
D0.2
-
1. 已知{an}是等差数列,且a2=-2,a4=-1. (Ⅰ)求{an}的通项公式; (Ⅱ)求{an}的前n项和Sn.
-
2. 设函数f(x)=x3+x-1.(Ⅰ)求f(x)的单调区间;(Ⅱ)求出一个区间(a,b),使得f(x)在区间(a,b)存在零点,且b-a<0.5.
-
3. 已知椭圆E的中心在坐标原点O,焦点在x轴上,长轴长为8,焦距为
 .(Ⅰ)求E的标准方程;(Ⅱ)若以O为圆心的圆与E交于四点,且这四点为一个正方形的四个顶点,求该圆的半径.
.(Ⅰ)求E的标准方程;(Ⅱ)若以O为圆心的圆与E交于四点,且这四点为一个正方形的四个顶点,求该圆的半径.
-
4. 已知椭圆C的长轴长为4,两焦点分别为F1(-
 ,0),F2(
,0),F2( ,0)。 (1)求C的标准方程;(2)若P为C上一点,|PF1|-|PF2|=2,求cos∠F1PF2。
,0)。 (1)求C的标准方程;(2)若P为C上一点,|PF1|-|PF2|=2,求cos∠F1PF2。
-
1.
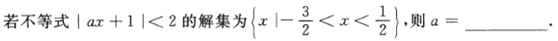
-
2. 张宏等5名志愿者分成两组,一组2人,另一组3人,则张宏被分在人数较多的一组的分法共_____有种。
相关试卷
-
2023年成考高起点每日一练《数学(理)》7月17日1759人做过
-
2023年成考高起点每日一练《数学(理)》7月18日440人做过
-
2023年成考高起点每日一练《数学(理)》7月19日488人做过
-
2023年成考高起点每日一练《数学(理)》7月20日177人做过
-
2023年成考高起点每日一练《数学(理)》7月21日927人做过
-
2023年成考高起点每日一练《数学(理)》7月22日855人做过
-
2023年成考高起点每日一练《数学(理)》7月23日613人做过
-
2023年成考高起点每日一练《数学(理)》7月24日1036人做过
-
2023年成考高起点每日一练《数学(理)》7月25日1201人做过
-
2023年成考高起点每日一练《数学(理)》7月26日1975人做过
相关题库