2024年成考高起点每日一练《数学(文史)》10月6日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:184
试卷答案:有
试卷介绍: 2024年成考高起点每日一练《数学(文史)》10月6日专为备考2024年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 设集合M={1,2,3,4,5},N={2,4,6},T={4,5,6}则(M∩T)∪N是()。
A{2,4,5,6}
B{4,5,6}
C{1,2,3,4,5,6}
D{2,4,6}
-
2. 从13名学生中选出2人担任正副班长,不同的选举结果共有()。
A26
B78
C156
D169
-
3. 设集合M={-2,0,2},N={0},则()。
AN为空集
BN∈M
C

D

-
4. 已知一个等差数列的第五项等于10,前三项的和等于3,那么这个等差数列的公差为()。
A3
B1
C-1
D-3
-
1. 设椭圆的中心是坐标原点,长袖在x轴上,离心率
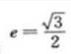 ,已知点P(0,3/2)到椭圆上的点的最远距离是
,已知点P(0,3/2)到椭圆上的点的最远距离是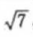 ,求椭圆的方程。
,求椭圆的方程。
-
2. 如图9-4,已知测速站P到公路L的距离为40米,一辆汽车在公路L上行驶,测得此车从A点行驶到8点所用的时间为2秒,并测得∠APO=60°,∠BPO=30°,计算此车从A到B的平均速度为多少km/h(结果保留到个位),并判断此车是否超过了80km/h的限制速度。

-
3. 如图:已知在△ADC中,∠C=90°,∠D=30°,∠ABC=45°,BD=20,求AC(用小数表示,保留一位小数)

-
4. 已知F是椭圆
 的右焦点,点M在抛物线y2=2px(p>0)上O为坐标原点,且△MOF为正三角形.
(Ⅰ)求P的值; (Ⅱ)求抛物线的焦点坐标和准线方程.
的右焦点,点M在抛物线y2=2px(p>0)上O为坐标原点,且△MOF为正三角形.
(Ⅰ)求P的值; (Ⅱ)求抛物线的焦点坐标和准线方程.
-
1. 函数f(x)=
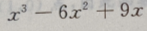 在区间[-3,3]上的最大值为()
在区间[-3,3]上的最大值为()
-
2.
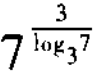 =______。
=______。
相关试卷
-
2024年成考高起点每日一练《数学(文史)》3月14日1068人做过
-
2024年成考高起点每日一练《数学(文史)》3月15日1222人做过
-
2024年成考高起点每日一练《数学(文史)》3月16日1501人做过
-
2024年成考高起点每日一练《数学(文史)》3月17日776人做过
-
2024年成考高起点每日一练《数学(文史)》3月18日1229人做过
-
2024年成考高起点每日一练《数学(文史)》3月19日672人做过
-
2024年成考高起点每日一练《数学(文史)》3月20日1962人做过
-
2024年成考高起点每日一练《数学(文史)》3月21日499人做过
-
2024年成考高起点每日一练《数学(文史)》3月22日459人做过
-
2024年成考高起点每日一练《数学(文史)》3月23日1056人做过
相关题库