2024年成考高起点每日一练《数学(文史)》10月26日

• 1. 已知a，b为任意正实数，则下列等式中恒成立的是（）。

  Aa^b=b^a

  B2^a+b=2^a+2^b

  C

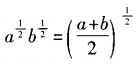
  Da^lgb=b^lga

• 2. 设甲：四边形ABCD是平行四边形，乙：四边形ABCD是正方形，则（）。

  A甲是乙的充分条件，但不是乙的必要条件

  B甲是乙的必要条件，但不是乙的充分条件

  C甲是乙的充分必要条件

  D甲不是乙的充分条件，也不是乙的必要条件

• 3. 已知等比数列a₁=1，a₉=25，则a₅=（）。

  A25

  B-5

  C±5

  D5

• 4. 设集合M={a，b，c，d}，N=（a，b，c），则集合M∪N=（）。  

  A{a，b，c}

  B{d}

  C{a，b，C，d}

  D空集

• 1. 已知等差数列前n项和 （Ⅰ）求通项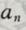的表达式 （Ⅱ）求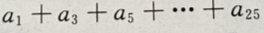的值  

• 2. 在△ABC中，已知AB=2,BC=1,CA= 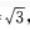点D,E,F分别在AB,BC,CA边上，△DEF为正三角形，记∠FEC为α，如果sinα= 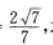求△DEF的边长。

• 3. 求证：双曲线的一个焦点到一条渐近线的距离等于虚半轴的长．  

• 4. 已知函数ƒ(x)=ax3-x2+bx+1(a，b∈R)在区间(-∞，0)和(1，+∞)上都是增函数，在(0，1)内是减函数． (Ⅰ)求a，b的值； (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程．

• 1. 与已知直线7x+24y-5=0平行，且距离等于3的直线方程是______。  

• 2. 袋中装有3个白球，2个红球，从中任取2个球，取到2个都是红球的概率是______。