2024年高职单招每日一练《数学》11月14日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:382
试卷答案:有
试卷介绍: 2024年高职单招每日一练《数学》11月14日专为备考2024年数学考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 圆内接菱形是正方形。()
A对
B错
-
2. 双曲线的离心率e小于1。()
A对
B错
-
1. 焦点(-5,0)和(5,0),虚轴长是6的双曲线的标准方程是()
A

B

C

D

-
2. 假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其2×2列联表为:
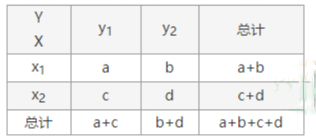 对同一样本,以下数据能说明X与Y有关的可能性最大的一组为()
(参考公式:
对同一样本,以下数据能说明X与Y有关的可能性最大的一组为()
(参考公式: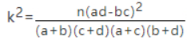 )
)
Aa=5,b=4,c=3,d=2
Ba=5,b=3,c=4,d=2
Ca=2,b=3,c=4,d=5
Da=3,b=2,c=4,d=5
-
1. 下列说法不正确的是()
A相切两圆的连心线经过切点
B长度相等的两条弧是等弧
C平分弦的直径垂直于弦
D相等的圆心角所对的弦相等
-
2. 设等差数列{an}的公差为d,其前n项和为Sn,且a1=-5,S3=-9,则()
Ad=2
BS2,S4,S6为等差数列
C数列
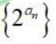 是等比数列
是等比数列DS3是Sn的最小值
-
1. 已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
-
2. 已知两直线
 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
-
1. 从4台甲型和5台乙型电视机中任意取出3台,其中至少要有甲型与乙型的电视机各1台,则不同的取法共有_______种.
-
2. 学校文艺队每个队员唱歌、跳舞至少会一门,已知会唱歌的有5人,会跳舞的有7人,现从中选3人,且至少要有一位既会唱歌又会跳舞的概率是
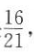 ,则该队有()人.
,则该队有()人.
相关试卷
-
2024年高职单招每日一练《数学》6月23日1377人做过
-
2024年高职单招每日一练《数学》6月24日1718人做过
-
2024年高职单招每日一练《数学》6月25日1046人做过
-
2024年高职单招每日一练《数学》6月26日2003人做过
-
2024年高职单招每日一练《数学》6月27日965人做过
-
2024年高职单招每日一练《数学》6月28日934人做过
-
2024年高职单招每日一练《数学》6月29日1854人做过
-
2024年高职单招每日一练《数学》6月30日1082人做过
-
2024年高职单招每日一练《数学》7月1日1729人做过
-
2024年高职单招每日一练《数学》7月2日658人做过
相关题库