2024年高职单招每日一练《数学(中职)》11月17日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:502
试卷答案:有
试卷介绍: 2024年高职单招每日一练《数学(中职)》11月17日专为备考2024年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 在等比数列{an}中,a2=4,a3=2,则该数列的前4项和S4=()
A7
B12
C13
D15
-
2. 已知tanα=-3,则cos²α-sin²α=()
A

B

C

D

-
3. 设首项为2,公比为2的等比数列{an}的前n项和为Sn,则()
A

B

C

D

-
4. 如图,在正方体ABCD-A1B1C1D1中,直线A1C与B1D1所成角的大小是()
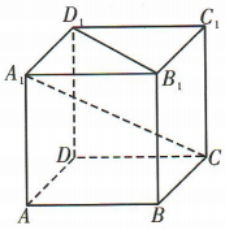
A30°
B45°
C60°
D90°
-
1. 已知函数f(x)=2x-m在[0,2]上的最小值为2,则f(m)=()
-
2. 已知|a|=2,|b|=4,a·b=-4,则向量a与b的夹角为()
-
3. 已知|a|=|b|=1,a与b的夹角为60°,则(a-2b)·a=()
-
4. 不等式
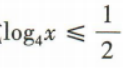 的解集为()
的解集为()
-
1. 已知a,b,c分别为△ABC的内角A,B,C的对边,且c2=2ab. (1)若C=90°,且a=1,求△ABC的面积; (2)若sinA=sinC,求cosC的值.
-
2. 如图,
 ,四边形 ABCD是矩形,E,F分别是CD,PB的中点,PD=8,BC=5.
,四边形 ABCD是矩形,E,F分别是CD,PB的中点,PD=8,BC=5.
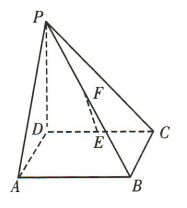 (1)证明EF//平面PAD:
(1)证明EF//平面PAD:
(2)求点P到 AB 的距离.
相关试卷
-
2024年高职单招每日一练《数学(中职)》10月7日1765人做过
-
2024年高职单招每日一练《数学(中职)》10月8日1714人做过
-
2024年高职单招每日一练《数学(中职)》10月9日1415人做过
-
2024年高职单招每日一练《数学(中职)》10月10日509人做过
-
2024年高职单招每日一练《数学(中职)》10月11日1057人做过
-
2024年高职单招每日一练《数学(中职)》10月12日1857人做过
-
2024年高职单招每日一练《数学(中职)》10月13日297人做过
-
2024年高职单招每日一练《数学(中职)》10月14日1923人做过
-
2024年高职单招每日一练《数学(中职)》10月15日1980人做过
-
2024年高职单招每日一练《数学(中职)》10月16日1645人做过
相关题库