2024年高职单招每日一练《数学(中职)》12月17日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1887
试卷答案:有
试卷介绍: 2024年高职单招每日一练《数学(中职)》12月17日专为备考2024年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 在等比数列{an}中,a2=4,a3=2,则该数列的前4项和S4=()
A7
B12
C13
D15
-
2. 有三张卡片,第一张卡片的正反两面分别写有数字1,3,第二张卡片的正反两面分别写有数字 2,4,第三张卡片的正反两面分别写有数字5,7.现从这三张卡片中任取两张并排放在桌面上,两张卡片朝上一面的数字组成一个两位数,则所有不同两位数的个数是()
A8
B12
C18
D24
-
3. 下列函数在其定义域内单调递增的是()
A

B
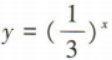
C
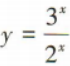
D
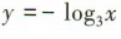
-
4. 函数
 的最小正周期是()
的最小正周期是()Aπ
B2π
C3π
D4π
-
1. 不等式
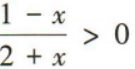 的解集为()
的解集为()
-
2. 若向量a与b共线,且|a|=|b|=1,则|a+b|=()
-
3. 已知数据x,8,y的平均数为8,则数据9,5,x,y,15 的平均数为()
-
4. 已知奇函数f(x)在[-3,0]上单调递减,且f(-3)=2,则f(x)在[0,3]上的最小值为()
-
1. 已知椭圆C的长轴长为10,两焦点F1,F2的坐标分别为(-3,0)和(3,0)(1)求椭圆的标准方程;
(2)若P为椭圆C上一点,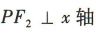 ,求△F1PF2的面积.
,求△F1PF2的面积.
-
2. 如图,四边形 ABCD是矩形,
 ,
, ,且AB=1,AD =MA = 2.
,且AB=1,AD =MA = 2.
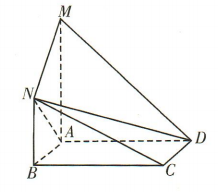 (1)证明:NC//平面MAD.
(1)证明:NC//平面MAD.
(2)求三棱锥M-NAD 的体积.
相关试卷
-
2024年高职单招每日一练《数学(中职)》12月23日1031人做过
-
2024年高职单招每日一练《数学(中职)》12月24日1088人做过
-
2024年高职单招每日一练《数学(中职)》12月25日1196人做过
-
2024年高职单招每日一练《数学(中职)》12月26日820人做过
-
2024年高职单招每日一练《数学(中职)》12月27日1520人做过
-
2024年高职单招每日一练《数学(中职)》12月28日1939人做过
-
2024年高职单招每日一练《数学(中职)》12月29日1540人做过
-
2024年高职单招每日一练《数学(中职)》12月30日1211人做过
-
2024年高职单招每日一练《数学(中职)》12月31日286人做过
-
2025年高职单招每日一练《数学(中职)》1月1日782人做过
相关题库