2024年成考高起点文科数学全真模拟卷(一)

• 1. 函数y=sinx/2sin(π/2-x/2)的最小正周期是（）。

  A4π

  Bπ

  C2π

  Dπ/2

• 2. 已知向量则实数m=（）。

  A1

  B-1

  C-4

  D4

• 3. 若函数y=f(x)的定义域是[-1,1]，那么f(2x-1)的定义域是（）。

  A[0，1]

  B[-3，1]

  C[-1，1]

  D[-1，0]

• 4. 若函数f(x)是奇函数，则函数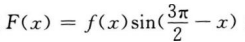的奇偶性是（）。

  A奇函数

  B偶函数

  C是非奇非偶函数

  D既是奇函数，又是偶函数

• 5. 设集合S={(x，y)｜xy>0｝，T={(x，y)｜x>0，且y>0｝，则()。

  AS∪T=S

  BS∪T=T

  CS∩T=S

  DS∩T=Ø

• 6. 已知f(x)是偶函数且满足f(x+3)=f（x）,f（1）=-1,则f（5）+f（11）等于（）。

  A-2

  B2

  C-1

  D1

• 7. 已知函数ƒ(x)的定义域为R，且满足ƒ(2x)=3x，则ƒ(x)的反函数为（）。

  Ay=log₂x³

  By=2log₃x

  C

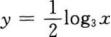
  D

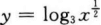
• 8. 命题甲：x＞y且xy＞0，命题乙：1/x＜1/y，则（）。

  A甲是乙的充分条件，但不是必要条件

  B甲是乙的必要条件，但不是充分条件

  C甲是乙的充分必要条件

  D甲不是乙的必要条件也不是乙的充分条件

• 9. 已知双曲线上一点到两焦点(-5，0)，(5，0)距离之差的绝对值等于6，则双曲线方程为（）。

  A

  B

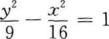
  C

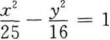
  D

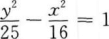
• 10. 已知二次函数y=ax²+bx+1的图像经过两点（-1,2）（2,5），则该图像也经过点（）。

  A（0,2）

  B（1,3）

  C（-2,1）

  D（3,10）

• 11. 等差数列{a_n｝中，a₁+a₂=15，a₃=-5，则前8项的和等于（）。

  A-60

  B-140

  C-175

  D-125

• 12. 若sin(π-α)=log₈1/4，且α∈(-π/2,0)，则cot(2π-α)的值为（）。

  A

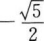
  B

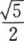
  C

  D

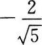
• 13. 函数f(x)=x²+2(m-1)x+2在区间(-∞,4)上是减函数,则实数m的取值范围是（）。

  Am≥-3

  Bm=-3

  Cm≤-3

  Dm≥3

• 14. 若直线l沿x轴负方向平移3个单位，再沿y轴正方向平移1个单位后，又回到原来的位置，则直线l的斜率是（）。

  A−1/3

  B-3 

  C1/3

  D3

• 15. 已知cos2a=5/13(3π/2＜a＜2π)，则tanα等于（）。

  A

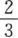
  B

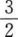
  C

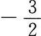
  D

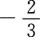
• 16. 已知直线L与直线2x-3y+5=0平行，则L的斜率为（）。

  A

  B

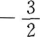
  C

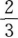
  D

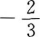
• 17. 甲袋内有2个白球3个黑球，乙袋内有3个白球1个黑球，现从两个袋内各摸出1个球，摸出的两个球都是白球的概率是（）。

  A2/5

  B3/4

  C3/10

  D4/9

• 1. 不等式|x+2|＜3的解集是（）。

• 2. 某小组有11名学生，其中女生4名，现选举2人当代表，要求至少有一名女生当选，则不同的选法有（）种。

• 3. 过点(1，2)且垂直于向量a=(-2，4)的直线方程为()。

• 4. 函数y=的定义域是（）。

• 1. 弹簧的伸长与下面所挂砝码的重量成正比，已知弹簧挂20g重的砝码时长度是12cm，挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度。

• 2. 如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC．(用小数表示，结果保留一位小数)。
  

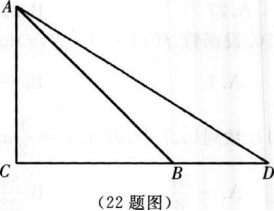
• 3. 已知数列 {a_n}中，S_n是它的前n项和，并且 S_n+1=4a_n+2，a1=1。（Ⅰ）设 b_n=a_n+1−2a_n，求证：数列{b_n}是等比数列；
  （Ⅱ）设 c_n=a_n/2ⁿ，求证：数列{c_n}是等差数列；
  （Ⅲ）求数列{a_n}的通项公式及前n项和。

• 4. 在△ABC中，已知三边a、b、c成等差数列，且最大角∠A是最小角的2倍，求a：b：c。