高职单招数学课后练习（3）函数

• 1. 下列函数中，在其定义域内既是偶函数，又在(-∞,0)上单调递增的函数是（  ）.  

  Af(x)=x²             

  Bf(x)=2^|x|

  Cf(x)=log_0.5|x|    

  Df(x)=sin2x

• 2. 若函数f(x)=x²+ax+3在（-∞，1]上单调递减，则实数a的取值范围是（  ）.  

  A(-∞,1]    

  B[―1，+∞)

  C(―∞，-2]

  D(-2,+∞)

• 3. 设f（x）是定义在R上的偶函数，当x≤0时，f(x)=2x²-x，则f(1)=(   )  

  A-3

  B-1

  C1

  D3

• 4. 函数y=lg(x+1)的定义域是（  ）.  

  A(-∞,-1)

  B(-∞,1)

  C(-1，+∞)

  D(1,-∞)

• 5. 若函数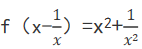，则f（x+1）等于（  ）.

  A

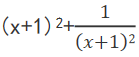
  B

  C(x+1)²+2

  D(x+1)²+1

• 6. 函数y=-(x-2)|x|的递增区间是（  ）.  

  A[0,1]

  B(-∞,1)

  C(1,+∞)

  D[0，1)和（2，+∞)

• 7. 设 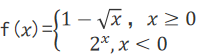,则f[f(-2)] =（  ）.

  A-1

  B1/4

  C1/2

  D3/2

• 1. 已知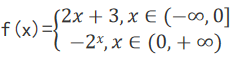则f[f(1)]=_____

• 2. 若f(x-1)= x²-2x+3,则f(x)=____________  

• 3. 函数y=x²+5的递减区间是____________  

• 4. 若函数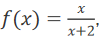则= _______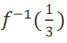

• 5. 若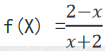，则f(2)=_______________

• 6. 已知函数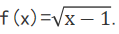若f(a)=3,则实数a=____________

• 1. 求k为何值时，二次函数f(x)=x²-(2k-1)x+(k-1)²的图像与x轴：（1）有2个不同的交点； （2）只有1个交点；（3）没有交点.

• 2. 2017年，某厂计划生产25吨至45吨的某种产品，已知生产该产品的总成本y(万元）与总产量x(吨）之间的关系可表示为 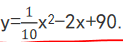(1)求该产品每吨的最低生产成本； (2)若该产品每吨的出厂价为6万元，求该厂2017年获得利润的最大值

• 3. 已知函数f(x)=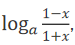(a>0,且a≠1) (1) 求函数f(x)的定义域; (2) 判断函数f(x)的奇偶性，并说明理由.  

• 4. 设函数f(x)既是R上的减函数，也是R上的奇函数，且f(1)=2.(1) 求f(-1)的值; (2) 若f(t²-3t+1)>-2，求t的取值范围  

• 5. 设函数f(x)是定义域为R上的奇函数，当x>0时， f(x)=x²−2x,求： （1）f(−2)；(2)求函数f(x)在R上的解析式.

• 6. 已知函数f(x)的定义域为{x|x≠0 },且满足f(x)+3f(1/x)=x .(1) 求函数f(x)的解析式; (2) 判断函数f(x)的奇偶性，并简单说明理由.