2025年成考高起点每日一练《数学(理)》1月17日

• 1. 中心在坐标原点，对称轴为坐标轴，且一个顶点（3，0），虚轴长为8的双曲线方程是（）

  A

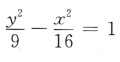
  B

  C

  D

• 2. 某车间有甲、乙两台机床，已知甲机床停机与不停机的概率为0.06，乙机床停机的概率为0.07，甲、乙两车床同时停机的概率是（）。

  A0.13

  B0.0042

  C0.03

  D0.04

• 3. sinθ·cosθ·tanθ<0，则θ属于集合（）。

  A{θ|<0<π}

  B{θ|<0<}

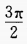  CØ

  D{θ|-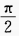<θ<0}

• 4. 若函数y=2^x-1+3的反函数的图像经过点P，则点P的坐标是（）。

  A(1，2)

  B(2，1)

  C(2，5)

  D(5，2)

• 1. 已知a^m=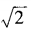，an=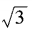，求a3^n-4m的值。  

• 2. 已知x+x^-1=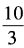，求x²+x-2的值。

• 3. 已知空间四边形OABC，OB=OC且∠AOB=∠AOC=θ（如图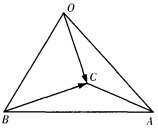）。求证：OA⊥BC。

• 4. 某工厂每月生产x台游戏机的收入为R(x)=+130x-206(百元)，成本函数为C(x)=50x+100(百元)，当每月生产多少台时,获利润最大?最大利润为多少?  

• 1. 曲线y=在点(1，1)处的切线方程是______。

• 2. y=cos²2x的最大值是______，最小值______，周期T=______。