2024成考专升本高等数学一模拟试卷(一)

• 1. 若级数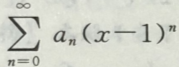在x=-1处收敛，则此级数在x=2处（）  

  A不能确定

  B绝对收敛

  C条件收敛

  D发散

• 2. 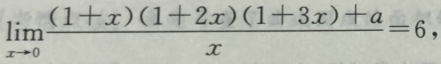则a的值为（）  

  A1

  B2

  C-1

  D

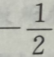
• 3. 设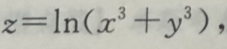则（）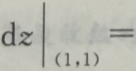  

  A

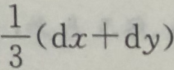
  Bdx+dy

  C

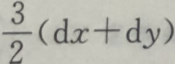
  D2(dx+dy)

• 4. 已知f(xy,x—y)=x²+y²，则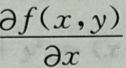等于（）  

  A2y

  B2x

  C2x+2y

  D2

• 5. 二元函数z=x³—y³+3x²+3y²—9x的极小值点为（）  

  A(1,0)

  B(1,2)

  C(-3,0)

  D(-3,2)

• 6. 方程x²+y²-z²=0表示的二次曲面是（）  

  A球面

  B圆锥面

  C旋转抛物面

  D圆柱面

• 7. 设函数f(x)=(1+x)e^x，则函数f(x)（）  

  A既有极小值又有极大值

  B有极大值

  C无极值

  D有极小值

• 8. 使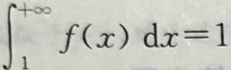成立的f(x)为（）  

  A

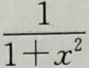
  B

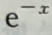
  C

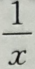
  D

• 9.

  A(-1,1)

  B(-∞,0]

  C(-∞,+∞)

  D[0,+∞)

• 10. 若f(x—1)=x²—1，则f'(x)等于（）  

  Ax(x—1)

  Bx(x+1)

  C2x—1

  D2x+2

• 1. 幂级数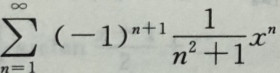的收敛半径R=（）.  

• 2. 函数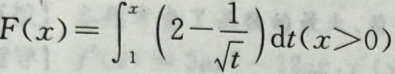的单调递减区间是（）.  

• 3. 设函数f(x)有连续的二阶导数且f(0）=0，f'(0)=1，f''(0)=-2，则（）.  

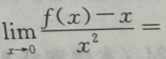• 4. 方程y'—e^x-y的通解为（）.  

• 5. 由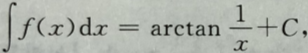求f(x)的导数等于（）.  

• 6. 设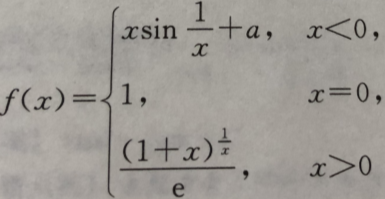在x=0处连续，则a=（）.  

• 7. 幂级数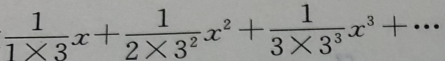的收敛半径为（）。  

• 8. 设f(x,y)=sin(xy²),则df(x,y)=（）。  

• 9. 已知z=(1+xy)^y,则（）.  

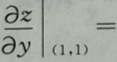• 10. 设f(x)=ax³—6ax³+b在区间[-1,2]的最大值为2，最小值为-29，又知a＞0，则a,b的取值为（）.  

• 1. 已知两直线和求过L₁且平行于L₂的平面的方程.  

• 2. 求  

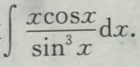
• 3. 求幂级数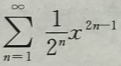的收敛区间.  

• 4. 求  

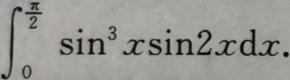
• 5.  

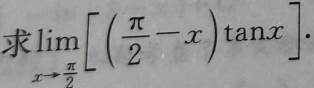
• 6. 证明：e^x＞1+x(x＞0).  

• 7. 计算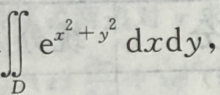其中D为x²+y²≤1，且x≥0，y≥0所围区域.  

• 8. 计算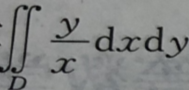，其中D是由y=x，y=2x，x=2与x=4围成.