2022年成考高起点每日一练《数学(理)》5月29日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1516
试卷答案:有
试卷介绍: 2022年成考高起点每日一练《数学(理)》5月29日专为备考2022年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 甲、乙、丙、丁、戊五个学生排成一排,甲必须排在乙之前的不同排法为()。
A

B
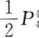
C
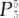
D
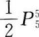
-
2. 已知平面α,两条直线l1,l2。设甲:l1⊥α且l2⊥α;
乙:l1//l2,
则()。A甲是乙的必要条件但不是充分条件
B甲是乙的充分条件但不是必要条件
C甲是乙的充要条件
D甲既不是乙的充分条件也不是乙的必要条件
-
3. 如果不共线的向量a和b有相等的长度,则
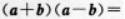 ( )
( )A0
B1
C-1
D2
-
4. 若向量a=(1,1),b=(1,-1),则
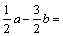 ()
()A(1,2)
B(-1,2)
C(1,-2)
D(-1,-2)
-
1. 正三棱柱ABC—A'B'C',底面边长为a,侧棱长为h。
(I)求点A到△A'BC所在平面的距离d;
(Ⅱ)在满足d=1的上述正三棱柱中,求侧面积的最小值。
-
2. 已知{an}为等差数列,且a3=a5+1. (Ⅰ)求{an}的公差d; (Ⅱ)若a1=2,求{an}的前20项和S20.
-
3. 在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积。
-
4. 某县位于沙漠边缘,到1999年底全县绿化率已达30%.从2000年开始,每年出现这样的局面:原有沙漠面积的16%被栽上树改为绿洲,而同时原有绿地面积的4%又被侵蚀,变为沙漠。(Ⅰ)设全县的面积为1,1999年底绿洲面积为a1=3/10,经过一年绿洲面积为a2,经过n年绿洲面积为an,求证:an+1=4/5an+4/25;
(Ⅱ)问至少经过多少年的绿化,才能使全县的绿洲面积超过60%(年取整数)。
-
1.

-
2. 曲线y=ex+x在点(0,1)处的切线方程为()。
相关试卷
-
2024年成考高起点每日一练《数学(理)》1月4日1454人做过
-
2024年成考高起点每日一练《数学(理)》1月5日1766人做过
-
2024年成考高起点每日一练《数学(理)》1月6日1307人做过
-
2024年成考高起点每日一练《数学(理)》1月7日895人做过
-
2024年成考高起点每日一练《数学(理)》1月8日1492人做过
-
2024年成考高起点每日一练《数学(理)》1月9日1128人做过
-
2024年成考高起点每日一练《数学(理)》1月10日1074人做过
-
2024年成考高起点每日一练《数学(理)》1月11日1179人做过
-
2024年成考高起点每日一练《数学(理)》1月12日1823人做过
-
2024年成考高起点每日一练《数学(理)》1月13日927人做过
相关题库