2023年高职单招每日一练《数学》2月3日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1431
试卷答案:有
试卷介绍: 2023年高职单招每日一练《数学》2月3日专为备考2023年数学考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 若函数f(x)=3x2+bx-1(b∈R)是偶函数,则f(-1)=2.
A对
B错
-
2. 不等式x2-5x-6≤0的解集是(x|-2≤x≤3}.
A对
B错
-
1. “点M在曲线y=|x|上”是“点M到两坐标轴距离相等”的()
A充要条件
B必要不充分条件
C充分不必要条件
D既不充分又不必要条件
-
2.
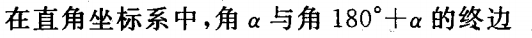 ()
()A一定关于x轴对称
B一定关于y轴对称
C一定关于原点对称
D
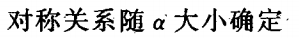
-
1. 拟发行体育奖券,号码从000001到999999,购置时揭号兑奖,若规定从个位数起,第一、三、五位是不同的奇数,第二、四、六位均为偶数时为中奖号码,则中奖率约为多少?(精确到0.1%)
-
2. 组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案共有多少种?
-
1. 若函数f(x+1)的定义域是[-1,1],则函数f(x)的定义域是().
-
2. 幂函数
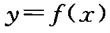 的图像经过点(2,1/4),则函数的解析式是_____。
的图像经过点(2,1/4),则函数的解析式是_____。
-
1. 数列{an}中,a1=1,an+1=1/3Sn(n∈N+),求: (1)a2、a3、a4的值; (2)求通项公式an
-
2. 函数
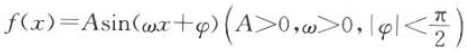 的部分图像如图所示. (1)求f(x)的最小正周期及解析式; (2)设g(x)=f(x)-cos 2x,求函数g(x)在区间
的部分图像如图所示. (1)求f(x)的最小正周期及解析式; (2)设g(x)=f(x)-cos 2x,求函数g(x)在区间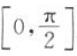 上的最大值和最小值.
上的最大值和最小值. 
相关试卷
-
2022年高职单招每日一练《数学》6月22日131人做过
-
2022年高职单招每日一练《数学》6月23日1980人做过
-
2022年高职单招每日一练《数学》6月24日1879人做过
-
2022年高职单招每日一练《数学》6月25日1365人做过
-
2022年高职单招每日一练《数学》6月26日1251人做过
-
2022年高职单招每日一练《数学》6月27日1487人做过
-
2022年高职单招每日一练《数学》6月28日139人做过
-
2022年高职单招每日一练《数学》6月29日290人做过
-
2022年高职单招每日一练《数学》6月30日1534人做过
-
2022年高职单招每日一练《数学》7月1日988人做过
相关题库