各校单招考试数学真题汇编卷(一)
考试总分:100分
考试类型:模拟试题
作答时间:90分钟
已答人数:17851
试卷答案:有
试卷介绍: 往年的湖南省各校单招考试数学真题已经整理好,需要备考的朋友们赶紧来刷题吧!
试卷预览
-
1. 已知平面向量a,b满足|a|=|b|=1,若|3a+2b|=
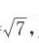 ,则向量a与b的夹角为()
,则向量a与b的夹角为() A

B

C

D

-
2. 已知平面向量a,b且满足a▪b=|a|=|b|=2,若e为平面单位向量,则|a▪e+b▪e|的最大值为().
A3
B
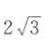
C4
D
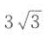
-
3. 已知平面向量a,b满足|a|=|a-b|=2,向量b在向量a方向上的投影为3,则向量a与向量b的夹角为().
A30°
B45°
C60°
D90°
-
4. 已知平面向量a,b是非零向量,|a|=2,a
 (a+2b),则向量b在向量a方向上的投影为().
(a+2b),则向量b在向量a方向上的投影为().A1
B-1
C2
D-2
-
5. 已知|a|=2,|b|=3,且=
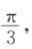 向量a,b的内积是().
向量a,b的内积是(). A
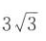
B3
C
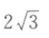
D
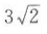
-
6. 已知平面向量a=(1,2),b=(x,-4).若a//b,则a▪b=().
A-6
B-10
C0
D6
-
7. 已知
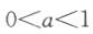 ,b<-1,则函数y=ax+b的图像必定不经过().
,b<-1,则函数y=ax+b的图像必定不经过().A第一象限
B第二象限
C第三象限
D第四象限
-
8. 已知f(x)的定义域是(0,1),则
 的定义域为().
的定义域为().A(0,1)
B
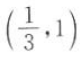
C(-∞,0)
D(0,+∞)
-
9. 函数
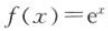 (e为自然对数的底)对任意实数x,y,都有().
(e为自然对数的底)对任意实数x,y,都有().Af(x+y)=f(x)f(y)
Bf(x+y)=f(x)+f(y)
Cf(xy)=f(x)f(y)
Df(xy)=f(x)+f(y)
-
10. 设平面向量a=(2,1),b=(0,-2),则与a+2b垂直的向量可以是().
A(4,-6)
B(4,6)
C(3,-2)
D(3.2)
-
11. 已知向量a=(1,2),b=(-1,-2),则a,b之间的位置关系是().
A平行
B不平行也不垂直
C垂直
D以上都不对
-
12. 已知平面向量a=(2,-1),b=(1,x).若a//b,则x=().
A
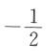
B-2
C
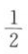
D2
-
13. 若向量
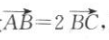 则下列各式中正确的是( )
则下列各式中正确的是( ) A
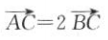
B

C
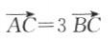
D
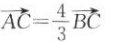
-
14. 如图所示,在正六边形ABCDEF中,向量


Aa-b
Bb-a
C2a-2b
D2b-2a
-
15. D,E,F分别为△ABC 的边BC,CA,AB上的中点,且
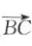 =a,
=a,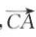 =b,下列 命题中正确的个数是( ).
①
=b,下列 命题中正确的个数是( ).
①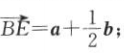 ②
②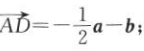 ③
③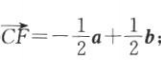 ④
④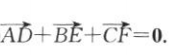
A1
B2
C3
D4
-
16. 化简

A

B
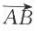
C

D

-
17. 如图所示,在平行四边形ABCD中,下列说法错误的是( ).
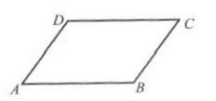
A
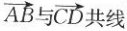
B
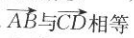
CA
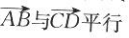
D
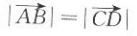
-
18. 已知点C是线段AB的中点,下面结论正确的是( ).
A

B
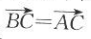
C
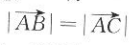
D
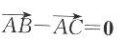
-
19. 如果→e1,→e2是平面内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基底的是()
A→e1与→e1+→e2
B→e1-2→e2与→e1+2→e2
C→e1+→e2与→e1-→e2
D→e1-2→e2与-→e1+2→e2
-
20. 有下列说法:①单位向量都平行;②零向量与任意向量都平行;③向量0是唯一没有方向的向量;④
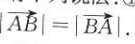 其中正确的是()
其中正确的是() A②④
B①③
C②③
D①④
-
1. 双曲线
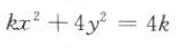 的离心率小于2,则k的取值范围是()
的离心率小于2,则k的取值范围是()
-
2. 若角β的终边经过点P(1,2),则sin β的值是().
-
3. 已知点P(tan α,cos α)在第三象限,则角α的终边在第()象限.
-
4. 设角
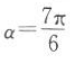 ,则其终边与单位圆交点的坐标为().
,则其终边与单位圆交点的坐标为().
-
5. 长半轴长为8,离心率为
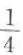 ,焦点在y轴上的椭圆的标准方程是()
,焦点在y轴上的椭圆的标准方程是()
-
6. 椭圆
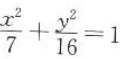 上一点M到椭圆的一个焦点的距离是1,则点M到另一个焦点的距离是()
上一点M到椭圆的一个焦点的距离是1,则点M到另一个焦点的距离是()
-
7. 椭圆
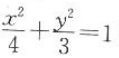 的焦点坐标是()
的焦点坐标是()
-
8. 椭圆9x2+y2=36的短轴长为()
-
9. 椭圆的标准方程是
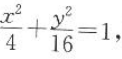 则椭圆的离心率是()
则椭圆的离心率是()
-
10. 幂函数
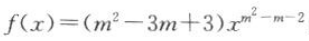 的图像不经过原点,则m=().
的图像不经过原点,则m=().
-
1. 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acos B.
(1)证明:A=2B;
(2)若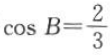 ,求cos C的值.
,求cos C的值.
-
2. 已知在△ABC中,
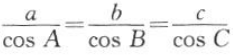 ,求证:△ABC是等边三角形.
,求证:△ABC是等边三角形.
-
3. 在△ABC中,D为BC边上一点,BD=33,
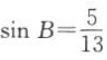 ,
, ,求AD.
,求AD.
-
4. 在△ABC中,BC=7,AB=3,且
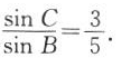
(1)求AC;
(2)求角A.
-
5. 抛物线的顶点在原点,圆x2+y2=4x的圆心恰好为抛物线的焦点. (1)求抛物线的方程; (2)一条斜率为2,且过抛物线焦点的直线依次交抛物线和圆于A,B,C,D四点,求|AB|与|CD|的和.
-
6. 若抛物线y2=2px(p>0)的准线与圆x2+y2-6x-7=0相切,求p的值.
-
7. 若抛物线y2=4x上的点P(m,n)到直线y=x的距离为
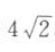 ,求
,求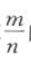 的值.
的值.
-
8. 抛物线的顶点在原点,对称轴为坐标轴,焦点在直线3x-4y-12=0上,求此抛物线的方程.
-
9. 函数
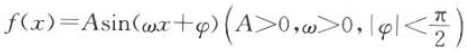 的部分图像如图所示. (1)求f(x)的最小正周期及解析式; (2)设g(x)=f(x)-cos 2x,求函数g(x)在区间
的部分图像如图所示. (1)求f(x)的最小正周期及解析式; (2)设g(x)=f(x)-cos 2x,求函数g(x)在区间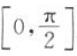 上的最大值和最小值.
上的最大值和最小值. 
-
10. 证明:函数
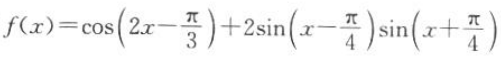 的最小正周期是π.
的最小正周期是π.
-
2024年高职单招每日一练《数学》6月23日1377人做过
-
2024年高职单招每日一练《数学》6月24日1718人做过
-
2024年高职单招每日一练《数学》6月25日1046人做过
-
2024年高职单招每日一练《数学》6月26日2003人做过
-
2024年高职单招每日一练《数学》6月27日965人做过
-
2024年高职单招每日一练《数学》6月28日934人做过
-
2024年高职单招每日一练《数学》6月29日1854人做过
-
2024年高职单招每日一练《数学》6月30日1082人做过
-
2024年高职单招每日一练《数学》7月1日1729人做过
-
2024年高职单招每日一练《数学》7月2日658人做过