各校单招考试数学真题汇编卷
考试总分:100分
考试类型:模拟试题
作答时间:90分钟
已答人数:3480
试卷答案:有
试卷介绍: 往年的四川省各校单招考试数学真题已经整理好,需要备考的朋友们赶紧来刷题吧!
试卷预览
-
1. 设A,B,C是△ABC的三个内角,下列关系恒成立的是().
Acos(A+B)=cos C
Bsin(A+B)=sin C
Ctan(A+B)=tan C
D
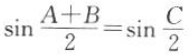
-
2. 集合
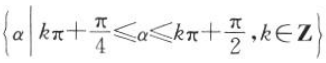 中的角所表示的范围(阴影部分)是().
中的角所表示的范围(阴影部分)是().A
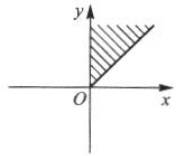
B
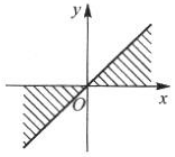
C
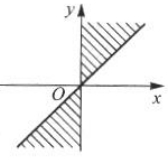
D
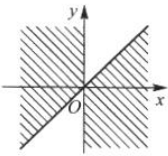
-
3. 若
 则角α的终边在().
则角α的终边在().A第一象限
B第二象限
C第三象限
D第四象限
-
4. 已知椭圆
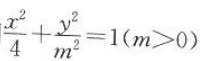 的离心率为
的离心率为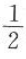 ,则m=().
,则m=(). A
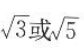
B
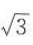
C
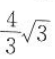
D

-
5. 已知F1,F2为椭圆
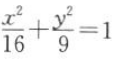 的两个焦点,过F2的直线与椭圆相交于M,N两点,则△MNF1的周长是().
的两个焦点,过F2的直线与椭圆相交于M,N两点,则△MNF1的周长是(). A16
B10
C8
D6
-
6. 若焦点在x轴上的椭圆
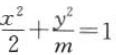 的离心率为
的离心率为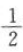 ,则m的值为().
,则m的值为(). A
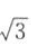
B

C
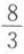
D
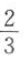
-
7. 已知椭圆
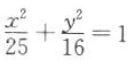 上的一点到椭圆一个焦点的距离为3,则该点到另一个焦点的距离为().
上的一点到椭圆一个焦点的距离为3,则该点到另一个焦点的距离为(). A2
B3
C5
D7
-
8. 若方程x²+ky²=2表示焦点在y轴上的椭圆,则实数k的取值范围为(),
A
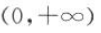
B(0,2)
C
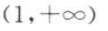
D(0.1)
-
9. 椭圆
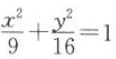 的焦点坐标为()。
的焦点坐标为()。 A
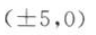
B
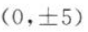
C
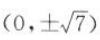
D
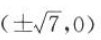
-
10. 某城市现有人口100万,根据最近20年的统计,这个城市的人口的年自然增长率为1.2%,按这个增长率计算,10年后这个城市的人口预计有()万.
A100×0.01210
B100×(1+1.2%)10
C100×(-1.2%)10
D100×1.210
-
11.
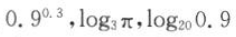 的大小关系为().
的大小关系为().A
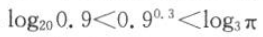
B
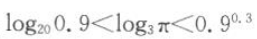
C
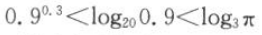
D
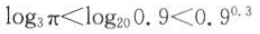
-
12. 若
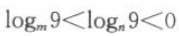 ,那么m,n满足的条件是().
,那么m,n满足的条件是().A
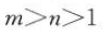
B
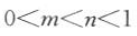
C
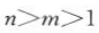
D
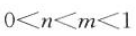
-
13. (-2)100+(-2)101等于().
A-1
B2100
C(-2)101
D-2100
-
14. 半径为4,且与y轴相切于原点的圆的方程为().
A

B
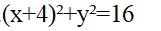
C
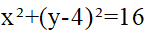
D

-
15. 直线3x+y-5=0与圆x2+y2-10y=0的位置关系是().
A相交
B相切 n
C相离
D无法确定
-
16. 以原点O为圆心,且截直线3x+4y+15=0所得弦长为8的圆的方程是().
A
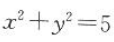
B
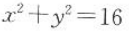
C
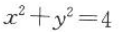
D
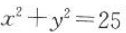
-
17. 已知圆O:x2+y2=4,直线l过点P(1,1),且与直线OP垂直,则直线l的方程为().
Ax+3y-4=0
By-1=0
Cx-y=0
Dx+y-2=0
-
18. 圆x2+y2+2x-4y+2=0的圆心坐标和半径分别为().
A(-1,2),3
B(1,-2),3
C(-1,2),

D(1,-2),
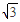
-
19. 由直线y=x+1上的一点向圆(x-3)²+y²=1引切线,则切线长的最小值为( ).
A1
B
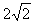
C
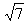
D3
-
20. 函数y=2.25x的图像经过点().
A(0,1)
B(1,0)
C(1,1)
D(2.25,1)
-
1. 在一次青年歌手大奖赛上,七位评委为某位歌手打出的分数为9.5,9.4,9.6,9.9,9.3,9.7,9.0.去掉一个最高分和一个最低分后,所剩数据的平均数是()。
-
2. 数据501,502,503,504,505,506,507,508,509的方差是()。
-
3. 广州市某电信分局管辖范围的电话号码由8位数字组成,其中前3位是一样的,后5位数字都是0~9这十个数字中的一个,那么该电信分局管辖范围内不同的电话号码个数最多为().
-
4. 3名医生和6名护士被分配到三所学校为学生体检,每校分配1名医生和2名护士,不同的分配方法共有()种.
-
5. (a+b)n+1的展开式中,奇数项的二项式系数之和为().
-
6. 函数
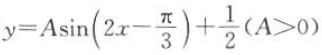 的最大值是
的最大值是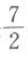 ,最小值是
,最小值是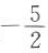 ,则A=().
,则A=().
-
7. 函数
 取得最大值时,对应的x的值为().
取得最大值时,对应的x的值为().
-
8. 函数
 的最大值是().
的最大值是().
-
9. 若
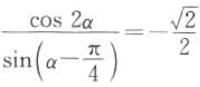 ,则sin α+cos α=().
,则sin α+cos α=().
-
10. 在△ABC中,若cos Acos B-sin Asin B=0,则△ABC是()三角形.
-
1. 在△ABC中,三个内角分别为A,B,C,它们所对的边分别为a,b,c.若asin A+bsin B=csin C,求证:△ABC为直角三角形.
-
2. 在△ABC中,已知a=2,
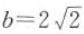 ,C=15°,求此三角形的角和边长.
,C=15°,求此三角形的角和边长.
-
3. 一个正方体的底面积和一个圆柱体的底面积相等,且侧面积相等,求正方体与圆柱体的体积比.
-
4. 如图所示,在直三棱柱ABC-A1B1C1中,AB=AC=3,BC=AA1=4,E,F分别是A1B,A1C的中点. (1)求证:EF//平面ABC; (2)求三棱锥E-ABC的体积.
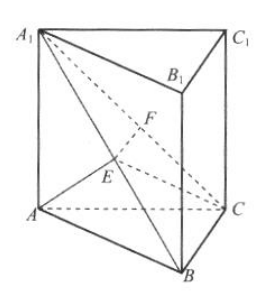
-
5. 如图所示,正方体ABCD-A1B1C1D1的棱长为1,求三棱锥B-ACB1的体积.
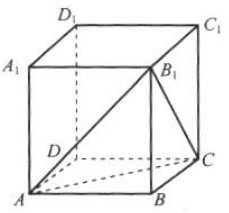
-
6. 已知棱长为3的正方体的顶点都在同一球面上,求该球的表面积.
-
7. 如图所示,三棱锥P-ABC的三条侧棱两两垂直,
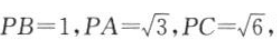 求其体积.
求其体积. 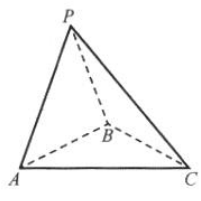
-
8. 如图所示,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上, 且
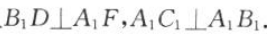 .求证: (1)直线DE//平面A1C1F; (2)平面B1DE
.求证: (1)直线DE//平面A1C1F; (2)平面B1DE 平面A1C1F.
平面A1C1F. 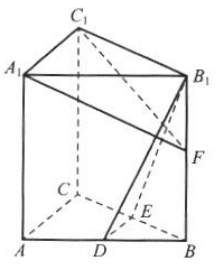
-
9. 如图所示,四棱锥P-ABCD中,底面ABCD是边长为2a的菱形,
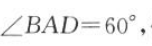 侧棱
侧棱 平面ABCD且PA=
平面ABCD且PA=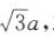 ,求二面角P-BD-A的大小.
,求二面角P-BD-A的大小. 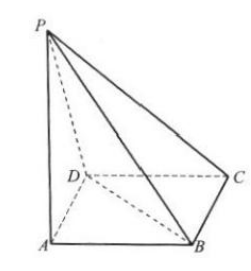
-
10. 如图所示,已知E,F,G,H分别是空间四边形ABCD边AB,AD,BC,CD上的点,且EF与GH相交于点P.求证:点B,D,P在同一直线上,
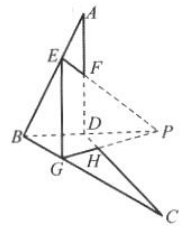
相关试卷
-
2024年高职单招每日一练《数学》5月7日1193人做过
-
2024年高职单招每日一练《数学》5月8日1894人做过
-
2024年高职单招每日一练《数学》5月9日246人做过
-
2024年高职单招每日一练《数学》5月10日573人做过
-
2024年高职单招每日一练《数学》5月11日1721人做过
-
2024年高职单招每日一练《数学》5月12日992人做过
-
2024年高职单招每日一练《数学》5月13日1002人做过
-
2024年高职单招每日一练《数学》5月14日1780人做过
-
2024年高职单招每日一练《数学》5月15日683人做过
-
2024年高职单招每日一练《数学》5月16日1642人做过
相关题库