2022年成考专升本高等数学一真题及答案

• 1. 当x→0时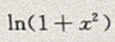，为x的（）  

  A高阶无穷小量

  B等价无穷小量

  C同阶但不等价无穷小量

  D低阶无穷小量

• 2.  

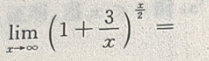
  A

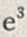
  B

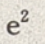
  C

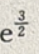
  D

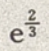
• 3. 设y^(n-2)=sinx，则y⁽ⁿ⁾=()  

  Acosx

  B-cosx

  Csinx

  D-sinx

• 4. 设函数f(x)=3x³+ax+7在x=1处取得极值，则a=（）  

  A9

  B3

  C-3

  D-9

• 5.  

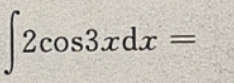
  A6sin3x+C

  B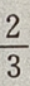sin3x+C

  Csin3x+C

  D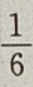sin3x+C

• 6.

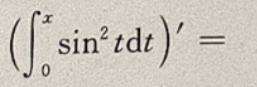
  Asin2x

  Bsin²x

  Ccos²x

  D-sin2x

• 7. 设z=(y-x)²+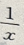，则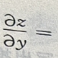

  A

  B

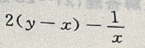
  C2(x-y)

  D2(y-x)

• 8. 函数f(x,y)=x²+y²-2x+2y+1的驻点是（）  

  A(0,0)

  B(-1,1)

  C(1,-1)

  D(1,1)

• 9. 下列四个点钟，在平面x+y-z+2=0上的是（）  

  A(-2,1,1)

  B(0,1,1)

  C(1,0,1)

  D(1,1,0)

• 10. 级数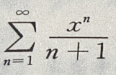的收敛半径为（）

  A

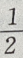
  B1

  C

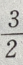
  D2

• 1.

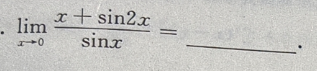
• 2. 设函数f(x)满足f’(1)=5，则

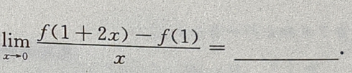
• 3. 设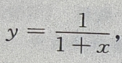则dy=（）  

• 4. 曲线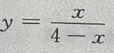的水平渐近线方程为（）  

• 5.

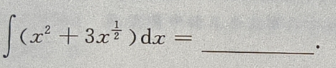
• 6.  

• 7.

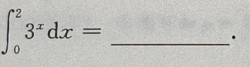
• 8. 设z=xtan(y²+1)，则（）

• 9. 微分方程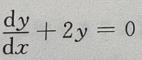的通解为y=（）  

• 10. 过点(1,0,-1)与平面3x-y-z-2=0平行的平面的方程为（）

• 1. 计算  

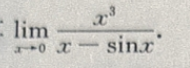
• 2. 设函数  

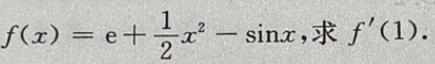
• 3. 求函数f(x)=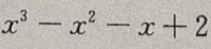的单调区间。  

• 4. 求曲线y=x²在点(1,1)处的切线方程。  

• 5. 求  

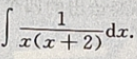
• 6. 求微分方程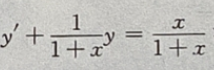满足初值条件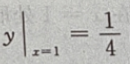的特解  

• 7. 计算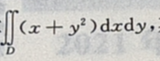其中D是由直线y=0.y=x,x=1所围成的闭区域。  

• 8. 证明：当x>0时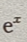>1+x.