2022年成考专升本高等数学二真题及答案
考试总分:150分
考试类型:模拟试题
作答时间:90分钟
已答人数:5174
试卷答案:有
试卷介绍: 2022年成考专升本高等数学二真题及答案已经整理好,需要备考的朋友们赶紧来刷题吧!
试卷预览
-
1. 设函数f(x)=sinx,g(x)=x2,则f(g(x))()
A是奇函数但不是周期函数
B是偶函数但不是周期函数
C既是奇函数又是周期函数
D既是偶函数又是周期函数
-
2. 若
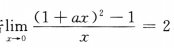 ,则a=()
,则a=()A 1
B 2
C 3
D4
-
3. 设函数f(x)在x=0处连续,g(x)在x = 0处不连续,则在x= 0处()
Af(x)g(x)连续
Bf(x)g(x)不连续
Cf(x)+g(x)连续
Df(x)+g(x)不连续
-
4. 设y=arccosx,则y'=()
A
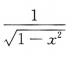
B
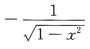
C
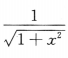
D
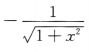
-
5. 设y=ln(x+e-x),则y'=()
A

B
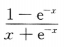
C
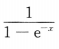
D
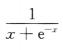
-
6. 设y(n-2)=x²+sinx,则y(n)=()
A2-sinx
B2-cosx
C2+sinx
D2+cosx
-
7. 若函数f(x)的导数f'(x)=-x+1,则()
Af(x)在(一∞,+∞)单调递减
Bf(x)在(一∞,+∞)单调递增
Cf(x)在(一∞,1)单调递增
Df(x)在(1,+∞)单调递增
-
8. 曲线
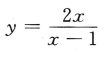 的水平渐近线方程为()
的水平渐近线方程为()Ay=0
By=1
Cy=2
Dy=3
-
9. 设函数f(x)=arctanx,则
 ()
()Aarctanx+C
B -arctanx +C
C
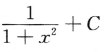
D

-
10. 设
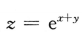 ,则
,则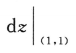 ()
()Adx+dy
Bdx+edy
Cedx+dy
De2dx+e2dy
-
1.
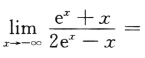 ()
()
-
2. 当x→0时,函数f(x)是x的高阶无穷小量,则
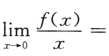 ()
()
-
3. 设y=3x2+ln3,则y'=()
-
4. 曲线y=x+√x在点(1,2)处的法线方程为()
-
5.
 ()
()
-
6.
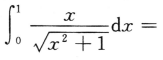 ()
()
-
7. 设函数
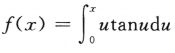 ,则
,则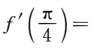 ()
()
-
8. 设z=x3y+xy3,则
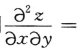 ()
()
-
9. 设函数z=f(u,v)具有连续偏导数,u=x+y,v=xy,则
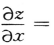 ()
()
-
10. 设A,B为两个随机事件,且P(A)=0.5,P(AB)=0.4,则P(B|A)=()
-
1. 设函数
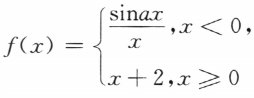 在x=0处连续,求a.
在x=0处连续,求a.
-
2. 设
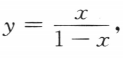 求y'.
求y'.
-
3. 求
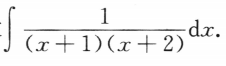
-
4. 计算
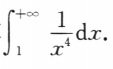
-
5. 设离散型随机变量X的概率分布为
 (1)求X的分布函数F(x);(2)求E(X).
(1)求X的分布函数F(x);(2)求E(X).
-
6. 设z=z(x,y)是由方程2y2+2xz+z2=1所确定的隐函数,求
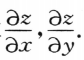
-
7. 设D为由曲线y=x2,y=0,x=2所围成的图形. (1)求D的面积; (2)求D绕x轴旋转一周所得旋转体的体积.
-
8. 证明:当x>1时,
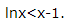
相关试卷
-
2024年成考专升本每日一练《高等数学二》1月21日460人做过
-
2024年成考专升本每日一练《高等数学二》1月22日174人做过
-
2024年成考专升本每日一练《高等数学二》1月23日1548人做过
-
2024年成考专升本每日一练《高等数学二》1月24日536人做过
-
2024年成考专升本每日一练《高等数学二》1月25日1939人做过
-
2024年成考专升本每日一练《高等数学二》1月26日179人做过
-
2024年成考专升本每日一练《高等数学二》1月27日461人做过
-
2024年成考专升本每日一练《高等数学二》1月28日1576人做过
-
2024年成考专升本每日一练《高等数学二》1月29日611人做过
-
2024年成考专升本每日一练《高等数学二》1月30日1460人做过
相关题库