已知m,n∈R,则“m≠0且n≠0”是“mn≠0”的()条件。
查看答案
相关试题
换一换


已知m,n∈R,则“m≠0且n≠0”是“mn≠0”的()条件。
答案
结肠癌临床分0~Ⅳ期,其中0期与T0、N0、M0对照。
A.正确 B.错误
答案
结肠癌临床分0~Ⅳ期,其中0期与T0、N0、M0对照()
答案
乳腺癌的TNM分期系统中,“T0”、“N0”、“M0”中下标的0的含义是:()
A.无(原发肿瘤、区域淋巴结转移、远处转移) B.(原发肿瘤、区域淋巴结转移、远处转移)无法评价 C.原位癌 D.无特殊含义,不允许这样标注
答案
已知点M(-1,1),N(0,0),则线段MN的长度为( )。
A.-2 B.2 C.4 D.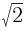
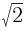
答案
对于常数m,n,mn0是方程mx2+ny2=1的曲线是椭圆的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
答案
T2-T4a,N0, M0的膀胱癌患者,其治疗的金标准为()
A.经尿道膀胱肿瘤电切术 B.膀胱部分切除术 C.全膀胱切除术 D.根治性膀胱全切+双侧盆腔淋巴 E.免疫生物治疗
答案
若m+n0,则下列结论正确的是( )。
A.m>0,n>0 B.m>0,n
答案
已知点M(0,-2)和点N(-3,2),则线段|MN|=( )。
A.3 B.4 C.5 D.6
答案
已知点M(0,-1),N(1,-1),则线段MN的长为( )。
A.2 B.3 C.1 D.4
答案
热门试题
按TNM分期法.第一期乳腺癌应为T1~T2,N0,M0。
已知点M(0,2),N(-6,-4),则线段MN中点的坐标是()
当FEC=3/4时,C0/N0=9.54DB,EBc/N0=()。
设一棵m叉树中度数为0的结点数为N0,度数为1的结点数为N1,,度数为m的结点数为Nm,则N0=()
设一棵m叉树中度数为0的结点数为N0,度数为1的结点数为Nl,……,度数为m的结点数为Nm,则N0=()。
设一棵m叉树中度数为0的结点数为N0,度数为1的结点数为Nl,……,度数为m的结点数为Nm,则N0=( )
M0:In some countries,such as the United Kingdom,M0 includes .
已知集合M={0,1,2,3},N={0,2,4,5},则M∩N=()
胃癌TNM分期中,T2N1M0中M0表示()
X~N(μ,σ2),H0∶μ=μ0,且σ2已知,则μ0的拒绝域为()。
若z=f(x,y)在点M0(x0,y0)可微,则z=f(x,y)在点M0(x0,y0)连续()
X0 在程序▕——▏▕——————[PLS M0]中,当X0接通时,M0接通
f(N)=O(g(n))表示当且仅当存在正的常数C和N0,使得对于所有的n>=N0,有()
M0—M15中M0数值都为1其它都为0那么K4M0数值等于多少()
M0—M15中,M0数值为1,其它都为0,那么,K4M0数值等于多少?()
在一棵二叉树中,度为0的结点数为n0,度为2的结点数为n2,则n0=()
设M,N为随机事件,P(N)0,且条件概率P(M|N)=1,则必有()。
设M,N为随机事件,P(N)>0,且条件概率P(M|N)=1,则必有()。
转子转速n与同步转速n0之差,与同步转速n0的比值称为转差率()
已知sinα<0且tanα<0,则α是()。



 使用微信扫一扫登录
使用微信扫一扫登录