设y=f(3x),其中f(x)为可导函数,则y′=().
查看答案
相关试题
换一换


设y=f(3x),其中f(x)为可导函数,则y′=().
答案
设函数y=f(x)在(0,+∞)内有界且可导,则( )。
A.当时,必有 B.当存在时,必有 C.当时,必有 D.当存在时,必有
答案
设函数y=f(x)在(0,+∞)内有界且可导,则( )。
A.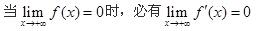 B.
B.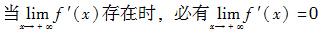 C.
C.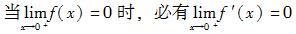 D.
D.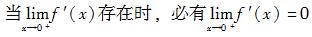
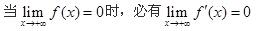 B.
B.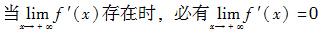 C.
C.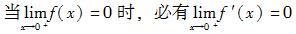 D.
D.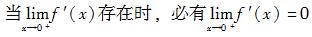
答案
设函数f(x)可导,则y=f{f[f(x)]}的导数为()
A.f′[f(x)] B.f′{f′[f′(x)]} C.f′{f[f(x)]}f′(x) D.f′{f[f(x)]}f′[f(x)]f′(x)
答案
设y=f(x)为可导函数,则当△x→0时,△y-dy为△x的( )
A.高阶无穷小 B.等价无穷小 C.同阶但不等价无穷小 D.低阶无穷小
答案
设方程x+z=yf(x2-z2)(其中f可微)确定了z=z(x,y),则z∂z/∂x+y∂z/∂y=( )。
A.x B.y C.z D.yf(x2-y2)
答案
设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=____。
答案
设函数 y=x3,则 y/=()
答案
设函数 y=x3,则 y/=()
答案
y=fx在点x0连续,则y=fx在点x0必定可导()
答案
热门试题
设f(x)是可导函数,且f′(x)=sin(x+1),f(0)=4,x=g(y)是y=f(x)的反函数,则g′(4)=().
设f(x,y,z)=exyz2,其中z=z(x,y)是由x+y+z+xyz=0确定的隐函数,则fx′(0,1,-1)=____。
设函数f(x,y)=x
3+y
3-3xy,则()。
设函数y=x3+ex,则y(4)=( )
设函数y=cos(3+2x),则y′′′=().
设函数z=z(x,y)由方程F(y/x,z/x)=0确定,其中F为可微函数,且F2′≠0,则x·(?z/?x)+y·(?z/?y)=( )。
设y=f(x2+a),其中f二阶可导,a为常数,则y"=()
设函数y=x2+3x+5,则y"=()
设X,Y是相互独立的随机变量,其分布函数分别为FX(x)、FY(y),则Z=min(X,Y)的分布函数是( )。
设单调函数y=y(x)二次可导,且满足微分方程d2y/dx2+(dy/dx)3=0,则其反函数x=x(y)满足方程d2x/dy2=1。
(2009)设y=f(x)是(a,b)内的可导函数,x △x是(a,b)内的任意两点,则:()
设y=f(x)是(a,b)内的可导函数,x+△x是(a,b)内的任意两点,则()
设y=f(x)是(a,b)内的可导函数,x,x+△x是(a,b)内的任意两点,则:
设可导函数f(x)满足xf′(x)-f(x)>0,则()。
设函数f(x)可导,且f(x)f"(x)>0,则
设函数f(x)可导,且f(x)f′(x)>0,则( )。
设(X,Y)~N(μ1,μ2,σ12,σ22,ρ),则随机变量X的边缘密度函数为fX(x)=____。
设函数y=(x-3)^4,则dy=()
设函数f(x)=|x^3-1|φ(x),其中φ(x)在x=1处连续,则φ(1)=0是f(x)在x=1处可导的( )。
设f(x)是可导函数,且f′(x)=sin2[sin(x+1)],f(0)=4,f(x)的反函数是x=φ(y),则φ′(4)=____。



 使用微信扫一扫登录
使用微信扫一扫登录