设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)>O,f’(x0)=0,则函数f(x)在点x0().
A. 取得极大值
B. 取得极小值
C. 的某个邻域内单调增加
D. 的某个邻域内单调减少
查看答案
相关试题
换一换


设y=f(x)是微分方程y´´-2y´+4y=0的一个解,又f(xo)>0,f´(xo)=0,则函数f(x)在点xo()
A.取得极大值 B.取得极小值 C.的某个邻域内单调增加 D.的某个邻域内单调减少
答案
设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)>O,f’(x0)=0,则函数f(x)在点x0().
A.取得极大值 B.取得极小值 C.的某个邻域内单调增加 D.的某个邻域内单调减少
答案
求微分方程y"-2y′-e2χ=0满足条件),y(0)=0,Y′(0)=1的解。
答案
设函数y=y(x)是微分方程y″+y′-2y=0的解,且在x=0处取得极值3,则y(x)=
答案
已知y0是微分方程y″+py′+qy=0的解,y1是微分方程y″+py′+qy=f(x)(f(x)≠0)的解,则下列函数中是微分方程y″+py′+qy=f(x)的解的是( )。
A.y=y0+C1y1(C1是任意常数) B.y=C1y1+C2y0(C1,C2是任意常数) C.y=y0+y1 D.y=2y1+3y0
答案
微分方程y′+y=e-xcosx满足条件y(0)=0的解为y=
答案
设函数y=f(x)是微分方程y″+y′-2y=0的解,且在x=0处y(x)取得极值3,则y(x)=
答案
已知y=e-3x是微分方程y”+4y'+ay=0的一个解,则常数a=()
A.1 B.-1 C.3 D.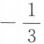
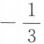
答案
微分方程y″-y′+y/4=0的通解为y=
答案
设y=f(x)是满足微分方程y″+y′-esinx=0的解,且f′(x0)=0,则f(x)在()
A.x0的某个邻域内单调增加 B.x0的某个邻域内单调减少 C.x0处取得极小值 D.x0处取得极大值
答案
热门试题
微分方程xy'+y=0满足y(1)=1的解为y=()
设y=ex是微分方程xy'+p(x)y=x的一个特解,求该微分方程满足条件y(ln2)=0的特解.
微分方程为xy′+y=0满足条件y(1)=1的解y=
求微分方程y"-y'-2y=0的通解.
微分方程y”+2y'+y=0的通解为()
微分方程y""+2y=0的通解是:
微分方程y″+2y=0的通解是( )。
微分方程yy″+(y′)2=0满足条件y(0)=1,y′(0)=0.5的特解是____。
微分方程y”-4y’+4y=0的通解为()
微分方程y'+4y=0的通解为()。
微分方程y”-2y'+5y=0的通解是().
微分方程y""+y=0的通解是 .
微分方程y''+y=0的通解是()。
设曲线y=y(x)上点P(0,4)处的切线垂直于直线x-2y+5=0,且该点满足微分方程y″+2y′+y=0,则此曲线方程为( )。
微分方程y″+[2/(1-y)](y′)2=0的通解为____。
微分方程y″+[2/(1-y)](y′)^2=0的通解为( )。
求微分方程y”-4y'+4y=0满足初始条件y(0)=3,y'(0)=9的特解.
微分方程y'+y=0的通解为y=
微分方程y"+y=0的通解为y=[]
微分方程y"+y=0的通解为y=



 使用微信扫一扫登录
使用微信扫一扫登录