在棱长为2的正方体中,M、N分别为棱AA´和BB´的中点,若θ为直线CM与D´N所成的角,则sinθ=( )。
A. 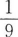 B.
B. 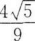 C.
C. 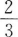 D.
D. 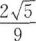
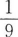
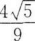
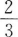
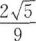
查看答案
相关试题
换一换


在棱长为2的正方体中,M、N分别为棱AA´和BB´的中点,若θ为直线CM与D´N所成的角,则sinθ=( )。
A.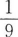 B.
B.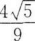 C.
C.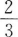 D.
D.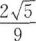
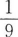 B.
B.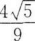 C.
C.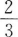 D.
D.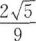
答案
若正方体的棱长是(1+2a)3,那么这个正方体的体积是()
A.(1+2a)6 B.(1+2a)9 C.(1+2a)12 D.(1+2a)27
答案
将一个棱长为5的正方体切割成多个小正方体,其中小正方体的棱长均为整数,那么所切割的小正方体中棱长为1的小正方体至少有多少个?
A.21 B.34 C.42 D.50
答案
已知正方体的棱长为2,则该正方体的全面积为()
A.8 B.12 C.16 D.24
答案
小正方体与大正方体的棱长比为1:3,小正方体与大正方体的体积比为()
A.1:27 B.1:9
答案
一个正方体的棱长之和是a厘米,它的棱长是()厘米
A.6a B.÷12 C.12a
答案
棱长1米的正方体的体积1()。
A.立方微米 B.立方厘米 C.立方分米 D.立方米
答案
正方体有12条棱,每条棱长度()
答案
正方体有12条棱,每条棱长度
答案
一个正方体棱长扩大2倍,体积就扩大()倍
A.2 B.4 C.8 D.16
答案
热门试题
体积是6的正方体,它的棱长是()
正方体的棱长为a,表面积S=_________,体积V=__________
正方体的对角线长为a,它的棱长为()
将2个棱长为30厘米的正方体木块的六面分别全涂成黑色后,都锯成棱长为10厘米的小正方体,问从这些小正方体中随机抽取出多少个,才能保证一定能够在取出的小立方体中挑出8个,拼成外表面全为黑色的,棱长为20厘米的正方体?
棱长为a厘米的正方体,其体积是()立方厘米
一个正方体的棱长是2cm,它的()是24cm2
正方体有几条棱跟几个顶点
把一个棱长是3厘米的正方体完全分割成若干个棱长小于3厘米但为整厘米数的小正方体,则最少可以分割成多少个小正方体()
一个正方体的棱长总和是60分米,它的棱长是( ),表面积是( ),体积是( )。
棱长是1米的正方体,体积是1立方米()
棱长是5 cm的正方体的表面积比体积大()
用一根长48厘米的铁丝折成了一个正方体框架,这个正方体的棱长是()厘米
两个棱长5cm的正方体拼成一个长方体,这个长方体的棱长总和是120cm()
一个正方体的表面积是384平方厘米,则这个正方体的棱长为______
将两个棱长为30厘米的正方体木块的六面全涂成黑色后,都锯成棱长为10厘米的小正方体,问从这些小正方体中随机抽取出多少个,才能保证一定能够在取出的小立方体中挑出8个,拼成外表面全为黑色的,棱长为20厘米的正方体?()
将两个棱长为30厘米的正方体木块的六面全涂成黑色后,都锯成棱长为10厘米的小正方体,问从这些小正方体中随机抽取出多少个,才能保证一定能够在取出的小立方体中挑出8个,拼成外表面全为黑色的,棱长为20厘米的正方体?()
一个正方体的棱长增加了20%后,体积增加了:
一个正方体的棱长总和是48㎝,它的表面积是()
棱长1厘米的正方体的表面积是()平方厘米。
已知正方体的棱长为1,则内切球的表面积等于()



 使用微信扫一扫登录
使用微信扫一扫登录