已知集合A={-1,0,1,2},B={x| x<0},则A∩B=()
A. {1,2}
B. {-1}
C. {-1,1}
D. {0,1,2}
查看答案
相关试题
换一换


已知集合A={0, 1 , 2} , B={1, 4},那么集合A∪B等于( ).
A.{1} B.{4} C.{2,3} D.{0,1,2,4}
答案
已知集合A={x|-4≤x<2},B={x|-1
A.{x|-4
答案
已知集合M={x|x<1},则 ( )
A.-1∈M B.1∈M C.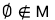 D.
D.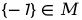
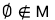 D.
D.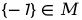
答案
已知集合A={1,2,3,4,5}.集合B={-2,2,3,4,5,9},则集合A∩B=()
A.{2,3,4} B.{2,3,4,5} C.{1,2,3,4,5} D.{-2,1,2,3,4,5}
答案
已知全集U为R,集合A={x│x≥1},那么集合CUA等于( ).
A.{x│x>1} B.{x│x>−1} C.{x│x<1} D.{x│x<−1}
答案
已知集合A={1,3,5,7},集合b={2,3,4,5},那么A∩B=()
A.{2,3,4} B.{3,4} C.{3,5} D.{2,3,5}
答案
已知集合M={x∈N|4-x∈N},则集合M中元素个数是
A.2 B.3 C.4 D.5
答案
已知集合A={0,1,2,3,4,5,6},集合B={x|x=3a,a∈A},A∩B=()
A.{3,6} B.{0,3,6} C.{0,2,6} D.{0,3}
答案
已知集合A={3,4},则A的子集有( )
A.4个 B.3个 C.2个 D.0个
答案
已知集合A{x|1≤x<2}集合B={x|2≤x<3}则下列关系正确的是
A.A∩B=∅ B.A∩B={2} C.A∪B={x|1<x<3} D.A∪B={x|1<x<2}
答案
热门试题
已知集合A={0,1,2,3,4},B={x()
已知集合A={3,4},则A的真子集有( )
已知集合A={1,4}则A的子集有( )个.
已知集合A={0,4}则A的子集有( )个.
已知:集合M={(x,y)│x+y=2},N={(x,y)│x−y=4},那么集合M∩N等于( )
已知集合A={(x,y)|x+2y=4},集合B={(x,y)|2x-y=3},则A∩B=().
已知集合A={1,2,3},则A的子集有( )个
已知集合A={1,4}则A的真子集有( )个.
已知集合A={0,4}则A的真子集有( )个.
已知集合A={1.2.3},B={a,3.4}.若A∩B={2,3},则a=()
已知泛型集合Listalist,数据3,3.5,“张三”均可以加入到alist集合中()
已知集合,={x|x2-2021x≤0},N={-1,0,1,2},则集合M∩N=()
已知集合A={1,m},B={2,3},A ∩B={2},则A∪B=_____。
已知集合A={x│x>2},B={x│0<x<4},则A∪B=( )
已知集合A={1,m},B={2,3},A ∩B={2},则A∪B=_____。
已知集合A={1,2,3},则A的真子集有( )个
已知集合A={1,2,3,4},则A的子集有( )个
已知集合A={1,2},B={2,3},则A∩B={2}
已知集合A={0,1},B={1,2},则A∩B={1}。
已知集合A={1,2,3},B={2,4},则A∪B=()



 使用微信扫一扫登录
使用微信扫一扫登录