已知向量a=(x,1),b=(2,-2),且a//b,则x的值为()
A. 1
B. 4
C. -1
D. -4
查看答案
相关试题
换一换


已知向量a=(x,1),b=(2,-2),且a//b,则x的值为()
A.1 B.4 C.-1 D.-4
答案
已知随机变量X~N(2,22),且Y=aX+b~N(0,1),则( )。
A.a = 2,b = -2 B.a = -2,b = -1 C.a = 1/2,b = -1 D.a =1/2,b = 1
答案
已知向量a=(3,2),b=(-4,x),且a⊥b,则x=()
答案
已知向量a=(3,2),b=(-4,x),且a⊥b,则x=()。
答案
已知向量a=(-2,x),b=(y,-1),c=(-4,2),且a⊥b,b//c,则()
A.x=4,y=-2 B.x=4,y=2 C.x=-4,y=-2 D.x=-4,y=2
答案
已知向量a=(1,-1),b=(2,x),若a·b=5,则x=()
A.-1 B.3 C.-3 D.1
答案
已知向量a⊥b,a=(-1,2),b=(x,2),则x=( )
A.4 B.-8 C.8 D.-4
答案
已知平面向量a=(2,-1),b=(1,x).若a//b,则x=().
A.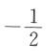 B.-2 C.
B.-2 C.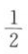 D.2
D.2
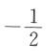 B.-2 C.
B.-2 C.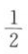 D.2
D.2 答案
已知点A(-2,-1),B(a,3),且|AB|=5,则a的值为()
A.1 B.-5 C.-1或-5 D.1或-5
答案
若向量a=(1,-1),b=(1,x),且|a+b|=2,则x=()。
A.-4 B.-1 C.1 D.4
答案
热门试题
已知向量a=(-3,1),b=(x,9),若a⊥b,则x=( )。
已知向量a=(5,1),b=(x,-2),若a⊥b,则x=()
已知向量a=(6,0,-3),b=(-2,9,x),且a⊥b,则x=()。
若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
若平面向量a=(x,1),b=(1,-2),且a∥b,则x=________.
已知f(x)=x3+ax2+bx在x=-1处取得极小值-2,则a=____,b=____。
若向量a=(x,-2),b=(-2,1),且a//b,则x=()
若向量a=(x,-2),b=(-2,1),且a//b,则x=()。
设向量a=(2,1),b=(x,4),且a⊥b,则x=()
已知向量a={2,1,-2)与向量b={3,-2,x)垂直,则x=().
已知向量a=(1.m+2),b=(m,-1),且a//b,则|b|=()
已知f(x)=x^3+ax^2+bx在x=-1处取得极小值-2,则a=( ),b=( )。
若平面向量a=(x,1),&=(1,-2),且a//b,则x=______.
已知向量a=(x,-3),b=(3,1),若a⊥b,则x=-9.
已知随机变量X服从正态分布N(2,22)且Y=aX+b服从标准正态分布,则()
已知A(5,-4),B(x,4),|AB|=10,则x的值为()
若平面向量a=(3,x),b=(4,-3),且a⊥b,则x的值等于( )
已知向量a={1,4,-4)与向量b={x,2,y}平行,则x+y=().
已知A(-1,0),B(2,2),C(0,y),如果向量AB垂直向量BC则y=()。
已知x=-1是函数(x)=ax3+bx2的驻点,且曲线y=(x)过点(1,5),求a,b的值.



 使用微信扫一扫登录
使用微信扫一扫登录