已知正四棱锥筒的上、下底边长分别为a、b,高为h,则其展开等腰梯形的高为()
A. 2/2
B. (b-a)/2-(b+a)2/4
C. h2-(b+(A)h
D. h2
查看答案
相关试题
换一换


已知正四棱锥筒的上、下底边长分别为a、b,高为h,则其展开等腰梯形的高为()
A.2/2 B.(b-a)/2-(b+a)2/4 C.h2-(b+(A)h D.h2
答案
已知正四棱锥的底面边长为4,侧棱长为3,则该四棱锥的侧面积为()
答案
若正四棱锥的底面每边长为3cm,高为5cm,则其体积为()
A.75cm3 B.5cm3 C.45cm3 D.15cm3
答案
侧棱长为2的正三棱锥,其底面边长是1,则棱锥的高是()。
A.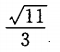 B.
B.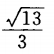 C.
C.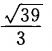 D.
D.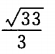
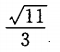 B.
B.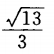 C.
C.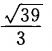 D.
D.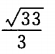
答案
若正四棱锥的底面每边长为3cm高为5cm,则其体积为()cm3
答案
若正四棱锥的底面每边长为3cm高为5cm,则其体积为__cm3
答案
已知正六棱锥底面的边长为2cm,侧棱长为4cm,求正六棱锥的体积。
答案
已知正六棱锥底面的边长为2cm,测棱长为4cm,求正六棱锥的体积。
答案
一个正三棱锥,高为1,底面三角形边长为3,则这个正三棱锥的体积为
A.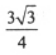 B.
B.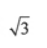 C.
C. D.
D.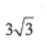
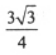 B.
B.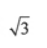 C.
C. D.
D.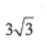
答案
正四棱锥底面边长为a,侧面积是底面积的2倍,则它的体积是_____.
答案
热门试题
已知,则直线AB的坐标方位角和边长分别为( )。
平面图形简易的面积计算:若正方形的边长为a,则面积A=a2;若长方形的边长分别为a和b,面积A=ab;若三角形的底边为b,高为h,则面积A=bh。()
梯形的上底、下底、高分别为a、b、h,则其面积为()。
太阳能突起路标的外形一般为梯形结构,下底边长规格有()
太阳能突起路标的外形一般为梯形结构,下底边长规格有()
正六棱柱放置位置为上下底面为水平面,前后两个侧面为正平面,则左右四个侧面为( )
过长方体一侧面的两条对角线交点,与下底面四个顶点连得一四棱锥,则四棱锥与长方体的体积比为多少?( )
已知正六棱柱的底面边长为10cm,高为15cm,则这个正六棱柱的侧面积为()
过正方体一侧面的两条对角线交点,与下底面四个顶点连得一四棱锥,则四棱锥与正方体的体积比是多少?()
某社区拟对一块梯形活动场地进行扩建,经测算,如果将梯形的上底边增加1米,下底边增加1米,则面积将扩大10平方米;如果将梯形的上底边增加1倍,下底边增加1米,则面积将扩大55平方米;如果将上底边增加1米,下底边增加1倍,则面积将扩大105平方米。现拟将梯形的上底边增加1倍还多2米,下底边增加3倍还多4米,则面积将扩大多少?
埃及胡福金字塔底边长()米、高()米。
画出一个正三棱锥的二视图,并标注尺寸(边长22)。
已知底边长度b和高度h的任意三角形的面积计算公式为()
如果AB两点的高差h为正,则说明()
正四棱锥的截面是一个()形。
有一个三棱锥,每个面均为边长为2的正三角形,已知该三棱锥的四个顶点位于同一个球面上,则此球的体积为:
已知AB两点的边长为188.43m,方位角为146°07′06″,则AB的x坐标增量为()
已知AB两点的边长为188.43m,方位角为146°07′06″,则AB的x坐标增量为()m
各棱长都为2的正四棱锥的体积为_______
已知AB两点间边长为:188.43m,AB的方位角为:146°07’00",则AB两点间的x坐标增量为()m。



 使用微信扫一扫登录
使用微信扫一扫登录