同时投掷两枚普通的骰子,所得两个点数之和大于9的概率是
查看答案
相关试题
换一换


同时投掷两枚普通的骰子,所得两个点数之和大于9的概率是
答案
同时抛掷两枚均匀的骰子1次,两枚骰子朝上面的点数之和大于8的概率是()。
答案
同时掷两枚骰子,所得点数之和为5的概率为( )
A.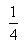 B.
B.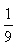 C.
C.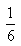 D.
D.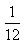
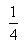 B.
B.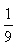 C.
C.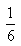 D.
D.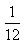
答案
抛掷两枚质地均匀的普通骰子,得到点数之和为2的概率是( )
A.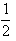 B.
B.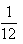 C.
C. D.
D.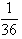
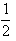 B.
B.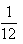 C.
C. D.
D.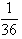
答案
抛掷两枚质地均匀的普通骰子,得到点数之和为10的概率是( )
A. B.
B.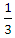 C.
C.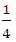 D.
D.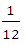
 B.
B.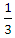 C.
C.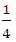 D.
D.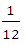
答案
投掷两枚质地均匀的正方体骰子,向上一面的点数之和为11的概率是().
A. B.
B.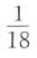 C.
C.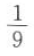 D.
D.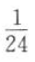
 B.
B.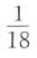 C.
C.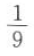 D.
D.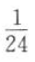
答案
抛掷两枚质地均匀的普通骰子,得到点数之积为6的概率是( )
A.1/4 B.1/6 C.1/9 D.1/36
答案
抛掷两枚质地均匀的普通骰子,得到点数之积为2的概率是( )
A. B.
B.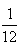 C.
C.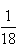 D.
D.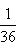
 B.
B.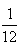 C.
C.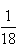 D.
D.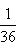
答案
同时投掷一枚硬币和骰子,硬币正面朝上且骰子点数大于4的概率是()。
A.1/6 B.1/3 C.1/2 D.2/3
答案
随机的抛掷三枚骰子,“有两枚筛子点数之和为11”的概率为(): 125/216|5/27|5/36|7/36
答案
热门试题
投掷两个骰子,点数之和为4(2≤r≤12),其组合数是多少()
抛两枚骰子,观察其点数之和,将可能的点数之和构成样本空间,则其中包含的样本点共有()。
1.写出下列随机试验的样本空间:(1)同时抛两个硬币,观察朝上正反面情况;(2)同时掷两个骰子,观察两枚骰子出现的点数之和;(3)生产产品直到得到10件正品为止,记录生产产品的总件数。
随意地投掷一均匀骰子两次,则两次出现的点数之和为8的概率为()。
同时抛掷两个质量均匀分布的骰子,抛出的点数和为9的概率是( )
同时抛掷两个质量均匀分布的骰子,抛出的点数和为9的概率是()
假设随意地投掷一均匀骰子两次,则两次出现的点数之和为8的概率为()
桌子上放有两枚质地均匀的骰子,均是1点朝上,现每次同时掷两枚骰子,规定拿走落下时偶数面朝上的骰子,保留落下时奇数面朝上的骰子,则掷骰子的次数多于三次的概率是( )。
抛掷两枚质地均匀的骰子一次,ξ为第一枚骰子掷出的点数与第二枚骰子掷出的点数之差,则ξ的所有可能的取值为()
投掷三枚均匀对称的硬币,恰有两枚正面朝上的概率是()
掷两颗骰子点数之和等于4的概率是()。
同时扔两个正常的骰子,即各面呈现的概率都是1/6,若点数之和为12,则得到的自信息为()。
掷两粒骰子,出现点数之和为5的概率为().
同时抛两枚1元硬币,出现两个正面的概率为1/4,其中“1/4”含义为____
一个正方体的骰子,六个面上分别有1,2,3,4,5,6个小圆点,随机投掷骰子两次,两次所得点数相加为5的概率是_______。
掷两个骰子,掷出的点数之和为奇数的概率为P1,掷出的点数之和为偶数的概率为P2,问P1和P2的大小关系是:
掷两个骰子,掷出的点数之和为奇数的概率为P1,掷出的点数之和为偶数的概率为P2,则P1和P2的大小关系为()
掷两个骰子,掷出的点数之和为奇数的概率为P1,掷出的点数之和为偶数的概率为P2,问P1和P2的大小关系是:
掷两个骰子,掷出的点数之和为奇数的概率为P1,掷出的点数之和为偶数的概率为P2,问P1和P2的大小关系?
掷两个骰子,掷出的点数之和为奇数的概率为P1,掷出的点数之和为偶数的概率为P2,P1和P2的大小关系为()



 使用微信扫一扫登录
使用微信扫一扫登录