∫[(4sinx+3cosx)/(sinx+2cosx)]dx=____。
查看答案
相关试题
换一换


\(\int_ {1}^{2}cosxdx+\int_ {2}^{4}cosxdx\\=\int_ {2}^{1}cosxdx+\int_ {4}^{2}cosxdx\)
答案
∫[(4sinx+3cosx)/(sinx+2cosx)]dx=()
A.2^x-ln|sinx+cosx|+C B.x^2-ln|sinx+cosx|+C C.x^2-ln|sinx+2cosx|+C D.2^x-ln|sinx+2cosx|+C
答案
∫[(4sinx+3cosx)/(sinx+2cosx)]dx=____。
答案
∫[(4sinx+3cosx)/(sinx+2cosx)]dx=( )。
A.2^x-ln|sinx+cosx|+C B.x^2-ln|sinx+cosx|+ C.x^2-ln|sinx+2cosx|+C D.2^x-ln|sinx+2cosx|+C
答案
cosxdx=d
答案
方程y(4)-y=ex+3sinx的特解应设为()。
A.ex+Bsinx B.ex+Bcosx+Csinx C.xex+Bcosx+Csinx D.x(Aex+Bcosx+Csinx)
答案
设sinx=1/2,则sin2xcos3x=()。
A.9/16 B.7/16 C.1/4 D.3/4
答案
函数y=4sinx+3在[-π,π]上的单调递增区间为()
A.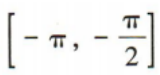 B.
B.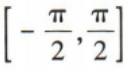 C.
C.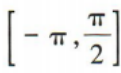 D.
D.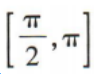
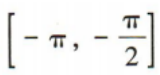 B.
B.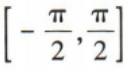 C.
C.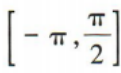 D.
D.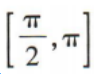
答案
求出两多项式函数P(x)、Q(x),使得下面等式成立: ∫[(2x4-1)cosx+(8x3-x2-1)sinx]dx=P(x)cosx+Q(x)sinx+C
答案
微分方程y(4)-y=ex+3sinx的特解可设为( )。
A.ex+Bcosx+Csinx B.xex+Bcosx+Csinx C.x(Aex+Bcosx+Csinx) D.ex+Bsinx
答案
热门试题
d=cosxdx , d=sinxdx
已知sinx=-1/3,在[0,2π)内的x值有()
微分方程y″+y=3sinx+4cosx的特解形式应设为:()
微分方程y″+y=3sinx+4cosx的特解形式应设为()
微分方程y^(4)-y=e^x+3sinx的特解可设为( )。
已知函数f(x)=(x+3)(x-a)为偶函数,函数g(x)=x3+4sinx+b+2为奇函数,则a+b的值为( )。
当x∈R时,函数y=2sinx+1的值域为[-1,3]。()
求函数f(x)=3cosx+4sinx的一阶导数为0的点。
有以下程序#includ#includvoifun(in**sinx[2][3]){ **s=*(x[1]+1); }main(){ ina[2][3{1,2,3,4,5,6}*p;(int*)malloc(sizeof(int));fun(&p,a);printf("%",*p);}程序的运行结果是()
计算∫excosxdx.
曲线y=(x+4sinx)/(5x-2cosx)的水平渐近线方程为____。
函数y=2sinx为( )。
已知sinx=a-4, 则a的取值范围( )。
函数f(x)=sinx+x3()
设y=3+sinx,则y=( )
设y=3+sinx,则y'=()。
设函数y=x3+sinx+3,求y".
∫[ln(sinx)/sin2x]dx=____。
已知sinx=2cosx,则tanx=( )。
设函数y=x4sinx,求dy.



 使用微信扫一扫登录
使用微信扫一扫登录