曲线y=x2与曲线y=alnx(a≠0)相切,则a=( )。
A. 4e
B. 3e
C. 2e
D. e
查看答案
相关试题
换一换


曲线y=x2与曲线y=alnx(a≠0)相切,则a=( )。
A.4e B.3e C.2e D.e
答案
设方程y´´-4y´+3y=0的某一积分曲线,它在点(0,2)处与直线x-y+2=0相切,则该积分曲线的方程是( ).
A.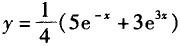 B.
B.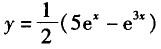 C.
C.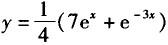 D.
D.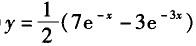
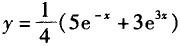 B.
B.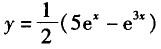 C.
C.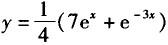 D.
D.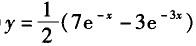
答案
设曲线y = x3+ax与曲线y= bx2+c在点(-1,0)处相切,则( )。
A.a=b=-1,c=1 B.a =-1,b=2,C=-2 C.a=1,b=-2,c=2 D.a=b =-1,c =-1
答案
若直线ax-y-2a-1=0与圆x²+y²-2x-1=0相切,则a的值是()
A.2 B. C.1 D.
C.1 D.
 C.1 D.
C.1 D.
答案
设f(x)在区间[0,+∞)内二阶可导且在x=1处与曲线y=x3-3相切,在(0,+∞)内与曲线y=x3-3有相同的凹向,则方程f(x)=0在(1,+∞)内有____个实根。
答案
求满足微分方程y”-12y'+36y=0的曲线,使其在点(0,1)处与直线y=5x+1相切.
答案
过点(1,0,0),(0,1,0),且与曲面z=x^2+y^2相切的平面为
A.Az=0与x+y-z=1 B.z=0与2x+2y-z=2 C.x=y与x+y-z=1 D.x=y与2x+2y-z=2
答案
过点P(5,0)与圆χ2+y2-4χ-5=0相切的直线方程是( )
A.y=5 B.χ=5 C.y=-5 D.χ=-5
答案
设曲线y=e2x+x-1在点(0,0)处与直线l相切,则直线l的斜率为()
A.不存在 B.1 C.3 D.-2
答案
直线x+y=0与圆x2+y2=1相切。
A.对 B.错
答案
热门试题
若抛物线x²=2py(p>0)的准线与圆x²+(y-2)²=25相切,则p的值为( ).
过点P(5,0)与圆x2+y2-4x-5=0相切的直线方程是( )
“c=1”是“直线x+y+c=0与圆(x﹣2)²+(y+1)²=2相切”的()
若直线3x+4y+k=0与圆x2+y2-6x+5=0相切,则k的值等于()
若直线x-y+m=0与圆x²+y²=1相切,则实数m的值为()
LAC曲线分别与各个SAC曲线的最低点相切。()
已知以P(1,2)为圆心,R为半径的圆与直线3X+4Y-7=0相切,则R为( )。
以点(1,-2)为圆心,且与直线x-y-1=0相切的圆的方程是()
长期平均成本曲线是一条与无数条短期平均成本曲线相切的曲线()
若圆x2+y2=c与直线x+y=1相切,则c=()
两曲线y=1/x,y=ax^2+b在点(2,1/2)处相切,则( )。
已知曲线y=x3-3a2x+b与x轴相切,则b2可以通过a表示为b2=____。
已知曲线y=ax4+bx3+x2+3在点(1,6)处与直线y=11x-5相切,求a,b.
在完全竞争的情况下,价格曲线与平均成本曲线相切是。
在LAC曲线与某条SAC曲线相切之点的产量上,必有()。
等产量曲线与等成本曲线相切时实现最优的生产要素组合()
在完全竞争的情况下,价格曲线与平均成本曲线相切是()
在完全竞争的情况下,需求曲线与平均成本曲线相切的是()。
在完全竞争的情况下,需求曲线与平均成本曲线相切点是()
若一直线的需求曲线与一曲线的需求曲线相切,则在切点处两曲线的需求弹性()



 使用微信扫一扫登录
使用微信扫一扫登录