已知α∩β=a,b⊥β,b在α内的射影是b’,那么b'和α的关系是()
A. b'//α
B. b'⊥α
C. b'与α是异面直线
D. b'与α相交成锐角
查看答案
相关试题
换一换


已知α∩β=a,b⊥β,b在a内的射影是b´,那么b´和a的关系是()。
A.b'∥a B.b'⊥a C.b'与a是异面直线 D.b'与a相交成锐角
答案
已知α∩β=a,b⊥β,b在α内的射影是b’,那么b'和α的关系是()
A.b'//α B.b'⊥α C.b'与α是异面直线 D.b'与α相交成锐角
答案
已知平面的一条斜线a和它在平面内的射影的夹角是45°,且另一平面内的直线b和斜线a在平面内的射影的夹角是 45°,则直线a、b所成的角α是 ( ).
A.30° B.45° C.60° D.90°
答案
如果“凡A不是B”,那么A与B的外延关系是()关系;如果“凡A是B并且凡B是A”,那么A与B的外延关系是()关系。
答案
已知a,b都是实数,那么“a2>b2”是“a>b”的( )。
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件
答案
已知平面a//β,过a内两点A、B分别向β引斜线AC、BD,使AC=37,BD=125,若AC在β的射影长是12,则BD在β内的射影长为_____.
答案
已知a<b,那么( )。
A.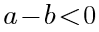 B.
B. C.
C. D.
D.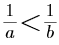
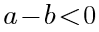 B.
B. C.
C. D.
D.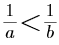
答案
如果直线a和直线b没有公共点,那么a与b的位置关系是()
A.相交 B.平行 C.异面直线 D.平行或异面
答案
已知“a=1b1;b=3b001;”那么{a,b}=()。
A.4b0011 B.3b001 C.4b1001 D.3b101
答案
已知 a =2’b10,b=3’b110,那么{a,b}=( )
答案
热门试题
已知非零向量a,b,且|a|=|b|,则a与b的关系是()
已知直线a,b,平面a,β.若a//a,b//a,则直线a,b的位置关系是().
设a、b是平面a外的任意两条线段,则“a、b的长相等”是“a、b在平面a内的射影长相等”的()
在△ABC中,已知B=60°,b2=ac,那么△ABC是().
已知a=00101010B和b=40D,下列关系式成立的是()
已知0.3×b<0.3,那么b一定是()
已知偶函数y=ƒ(x)在区间[a,b](0
如果所有a是b,那么a与b的外延关系可能是()。
如果所有A是B,那么A与B的外延关系可能是
已知平面向量a,b满足a=(1,-1),(a+b)⊥(a-b),那么|b|=_______。
如果有的A是B,有的A不是B,那么A与B外延间的关系是()
已知异面直线a,b分别在平面α,β内,α∩β=c,那么直线c( )
已知偶函数y=f(x)在区间[a,b](0
已知偶函数y=f(x),在区间[a,b](0
已知证券组合P是由证券A和B构成,证券A和B的期望收益、标准差以及相关系数如表7-8所示。{图}那么,()
若平面α||平面β,直线a⊂α,直线b⊂β那么直线a、b的位置关系是( )
中国大学MOOC: 已知 a =4’b1010,b=4’b1100,那么&(a & b)=( )
若a,b为有理数,a大于0,b小于0且∣a∣小于∣b∣,那么a,b,-a,-b的大小关系是
已知a+1/2 =b+1/3 ,则a与b的关系是()
已知集合A={0, 1 , 2} , B={1, 4},那么集合A∪B等于( ).



 使用微信扫一扫登录
使用微信扫一扫登录