相关试题
换一换


已知平面向量a=(1,1),b=(1,-1),则两向量的夹角为()。
A. B.
B.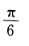 C.
C.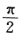 D.
D.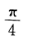
 B.
B.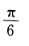 C.
C.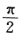 D.
D.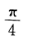
答案
已知平面向量a=(1,1),b=(1,-1),则两向量的夹角为( )
A. B.
B.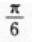 C.
C.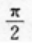 D.
D.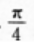
 B.
B.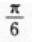 C.
C.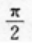 D.
D.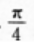
答案
已知平面向量a,b满足|a|=|a-b|=2,向量b在向量a方向上的投影为3,则向量a与向量b的夹角为().
A.30° B.45° C.60° D.90°
答案
已知平面向量a=(-1,2),b=(1,0),则向量3a+b=().
A.(2.6) B.(-2,-6) C.(-2.6) D.(2,-6)
答案
已知平面向量a,b满足(a+2b)▪a=0,则().
A.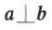 B.a//b C.
B.a//b C.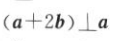 D.(a+2b)//a
D.(a+2b)//a
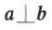 B.a//b C.
B.a//b C.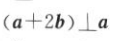 D.(a+2b)//a
D.(a+2b)//a 答案
已知平面向量a=(2,-1),b=(1,x).若a//b,则x=().
A.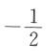 B.-2 C.
B.-2 C.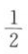 D.2
D.2
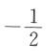 B.-2 C.
B.-2 C.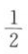 D.2
D.2 答案
已知平面向量a=(1,-1),b=(-1,2),则a+b=()
A.(0,1) B.(-2,3) C.(2,-3) D.1
答案
已知平面向量a=(1,2),b=(x,-4).若a//b,则a▪b=().
A.-6 B.-10 C.0 D.6
答案
已知平面向量a=(1,t),b=(-1,2),若a+b行于向量(-2,1),则( )
A.2t-3m+1=0 B.2t+3m+1=0 C.2t-3m-1=0 D.2t+3m-1=0
答案
已知平面向量ɑ=(-2,1)与b=(λ,2)垂直,则λ=( )
A.4 B.-4 C.-1 D.1
答案
热门试题
已知平面向量a=(-2,1)与b=(λ,2)垂直,则λ=( )
已知平面向量a=(-2,1)与b=(λ,2)垂直,则λ=()。
已知平面向量a(-2,1)与b= (A,2)垂直,则A=
已知平面向量a=(2,1),b=(-1,1),则a+b=
已知平面向量a=(2,1),b=(-1,1),则a+b=().
已知向量a,b满足|a|=7,|b|=12,a·b=-42,则向量a,b的夹角为()
已知向量a,b是夹角为60°的单位向量,则|a+b|=()
已知平面向量a,b且满足a▪b=|a|=|b|=2,若e为平面单位向量,则|a▪e+b▪e|的最大值为().
已知平面向量a=(1,t),b=(-1,2),若a+mb平行于向量(-2,1),则
已知向量a,b满足|a|=1,|b|=2,a·(a+b)=0,则向量a与b的夹角为()
已知平面向量a,b满足|a|=1,|b|=2,a·b=1,则|2a-b|的值为()
已知两个单位向量a,b的夹角是120°,则|a-b|=()
已知平面向量a,b满足a=(1,-1),(a+b)⊥(a-b),那么|b|=_______。
已知平面向量a=(l,2),b=(―2,3),2a+3b=________.
已知|a|=2,|b|=4,a·b=-4,则向量a与b的夹角为()
已知两个非零向量a和b满足a·b=0,则a与b的夹角为()
设平面向量a=(2,1),b=(0,-2),则与a+2b垂直的向量可以是().
已知平面向量a=(1,2),b=(3,6),则下列说法中正确的是().
若平面向量a=(x,1),b=(1,-2),且a∥b,则x=________.
若平面向量a=(x,1),b=(1,-2),且a//b,则x=()



 使用微信扫一扫登录
使用微信扫一扫登录