集合{x|x>-2且x≠2023}用区间可表示为( )。
A. (-2,2023)
B. (-2,+∞)
C. (-2,2023) ∪(2023,+∞)
D. (2023,+∞)
查看答案
相关试题
换一换


集合{x|x>-2且x≠2023}用区间可表示为( )。
A.(-2,2023) B.(-2,+∞) C.(-2,2023) ∪(2023,+∞) D.(2023,+∞)
答案
集合{x|x<2}可用区间表示为( )。
A.(﹣∞,2) B.(﹣∞,2] C.[2,+∞) D.(2,+∞)
答案
不等式x2-9≥0的解集用区间可表示为( )。
A.[3,+∞) B.[0,+∞ ) C.(-∞ ,-3]∪[3,+∞) D.(-∞,+∞]
答案
区间(-∞,2)∪(2,+∞)用集合表示为()
A.{xx>2} B.{xx<2} C.{xx≠2} D.{xx≥2}
答案
x为不小于5的实数用区间可表示为( )。
A.(5,+∞) B.[5, +∞) C.(- ∞,5) D.(- ∞,5]
答案
用列举法表示集合{(x,y)|x+2y=7且x,y为正整数},结果是()。
A.{x=5,3,1,y=1,2,3} B.{(5,1),(3,2)(1,3)} C.{(1,5),(2,3),(3,1)} D.{(7,0)(5,1)(3,2)(1,3)}
答案
区间(-3,2]用集合表示正确的是( )。
A.{-2,-1,0,1,2} B.{-3,2} C.{x|-3<x<2} D.{x|-3<x 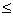 2}
2}
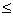 2}
2} 答案
实际值用A表示时()可表示为Δx=x-A
A.相对误差 B.基本误差 C.自身误差 D.绝对误差
答案
实际值用A表示时()可表示为:△x=x-A。
A.相对误差 B.绝对误差 C.人身误差 D.基本误差
答案
0≤x<2用区间表示为()。
A.[0,2) B.(0,2) C.[0,2] D.(0,2]
答案
热门试题
已知-1x+y4且2x-y3,则z=2x-3y的取值范围是 .(答案用区间表示)
设集合 M={xx<1},N={yy=2x,x∈M}, ,则集合CR(M∩N)等于()
区间(﹣7,2 ]可用集合表示为( )。
不等式x^2<25的解集用区间表示为______
满足不等式a≤x≤b的实数x的集合叫闭区间,表示为(a,b)。()
方程x2+2x-3=0的解集可表示为{-1,3}。
下列区间表示数集{x|-2≤x<5}的是()
曲线y=x(x-1)(2-x)与x轴所围成的平面图形的面积可表示为()。
AGC用中文可表示为()
平面区域D={(x,y)|x2+y2≤2y}在极坐标系下可表示为().
码分多址用英文缩写可表示为()
电容值用公式可表示为()
设函数f(x)在区间[-2,2]上可导,且f′(x)>f(x)>0,则( )。
已知集合A={x|x<2a-1},B={x|x≥1},且A∪B=R,则实数a的取值范围是()
集合A={x|0≤x≤2},B={x|x≥1}则集合A∩B=()。
设集合M=(x||x|<2},N=(x||x-1|>2},则集合M∩N=()
设集合M=(x||x|<2},N=(x||x-1|>2},则集合M∩N=()
基金估值用公式可表示为( )。
由属性集X函数决定的属性的集合称为(),用符号()表示。
1升溶液中含H2SO498.08g,用物质的量浓度表示,可表示为()



 使用微信扫一扫登录
使用微信扫一扫登录