已知二次函数f(x)的二次项系数为实数a,且其图像与直线2x+y=0交点横坐标为1和3.
(1)若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数n的取值范围.
查看答案
相关试题
换一换


已知二次函数f(x)的二次项系数为实数a,且其图像与直线2x+y=0交点横坐标为1和3. (1)若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式; (2)若f(x)的最大值为正数,求实数n的取值范围.
答案
已知二次函数f(x)的二次项系数为实数a,且其图像与直线2x+y=0交点横坐标为1和3. (1)若方程f(x)+6a=0有两个相等的实数根,求f(x)的解析式; (2)若f(x)的最大值为正数,求实数n的取值范围.
答案
如果二次函数的图像经过原点和点(-4,0),则该第二次函数图像的对称轴方程
答案
如果二次函数的图像经过原点和点(-4,0),则该第二次函数图像的对称轴方程为______
答案
已知一个二次函数的顶点坐标为(0,4),且过(1,5)点,则这个二次函数的解析式为()
A.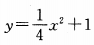 B.
B.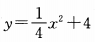 C.
C.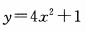 D.
D.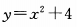
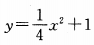 B.
B.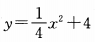 C.
C.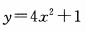 D.
D.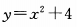
答案
二次函数y=2x(x-1)的一次项系数是()
A.1 B.-1 C.2 D.-2
答案
二次规划的正确说法是:目标函数为线性函数,约束中存在二次函数()
A.正确 B.错误
答案
已知二次函数y=x2+ax+1在区间[1,+∞)上为递增函数,则实数a的取值范围是( )
A.a≥-2 B.a≤-2 C.a≥-1 D.a≤-1
答案
已知二次函数f(x)=x2+ax+1,且f(1)=f(3),则a=()
A.-4 B.-2 C.2 D.4
答案
将二次函数y=1/3(x-2)2-4的图像先向上平移三个单位,再向左平移五个单位,所得图像对应的二次函数解析式为()。
答案
热门试题
二次函数y=x2+x-2的图像与z轴的交点坐标为( )
下列函数中,不是二次函数的是()
已知一次函数y=kx+b的图像关于原点对称,则二次函数y=ax2+bx+c(a≠0)一定是()
“二次打击”学说的观点认为第二次打击与第一次相比其作用
二次函数y=x2+x-2的图像与x轴的交点坐标为()。
二次函数y=x2+x-2的图像与x轴的交点坐标为 ( )
二次风调整时,下二次风量比上二次风量要()。
二次风调整时,下二次风量比上二次风量要()
已知二次函数f(x)=x²+4x+2的顶点坐标是( )
测得某线路二次功率值与实际二次值相比明显偏小,其可能的原因()
已知函数y=ax²+bx+c的图像经过点A(-5,0),B(0,-5)两点,它的对称轴为直线x=5,求二次函数的解析式。
二次申诉复核只针对首次投诉后()且二次申诉内容明确()的快件
下列各选项中的点不在二次函数+6x图像上的是()
已知二次函数 f(x)=x2+bx+c的图像过点P(1,0),并且对于任意实数x,有f(1+x)=f(1-x),求函数f(x)的最值。
已知是正定二次型,则().
已知是正定二次型,则().
二次函数y=x2+2x+2图像的对称轴为 ( )
测得某线路二次功率值与实际二次值相比明显偏小,其可能的原因是()。
二次函数y=x²在(−∞,0)上是( )
二次设备利用与一次设备实现电气隔离,且二次绕组均接地,从而保证了设备和人身安全()



 使用微信扫一扫登录
使用微信扫一扫登录