已知函数f(x)=x2-2ax+3的值域是[-1,+∞),则a=()
查看答案
相关试题
换一换


已知函数f(x)=x2-2ax+3的值域是[-1,+∞),则a=()
答案
已知函数f(x)=ax³+bx+3满足f(1)=6.则f(-1)=()
答案
已知函数f(x)=ax³+bx+3,且f(-2)=1,则f(2)=()
A.-1 B.3 C.4 D.5
答案
已知函数f(x)=ax3.若f'(3)=9,则a=()。
A.  B.
B. 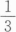 C.1 D.3
C.1 D.3
 B.
B. 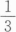 C.1 D.3
C.1 D.3 答案
已知函数f(x)=ax³+bx(a≠0)满足f(-3)=3,则f(3)=()
A.2 B.-2 C.-3 D.3
答案
已知函数f(x)=ax-2,f(-1)=2,则f(1)= ( ).
A.-2 B.2 C.-6 D.0
答案
函数f(x)=ax-2,已知f(-1)=2,则f(1)=( ).
A.-2 B.2 C.-6 D.0
答案
函数f(x)=ax-2,已知f(-1)=2,则f(1)=( ).
A.-2 B.2 C.-6 D.0
答案
已知y=f(x)是定义在区间[2,7]上的单调函数,值域为[1,5],则其反函数x=φ(y)的值域为()
A.[1,5] B.[2,7] C.(1,5] D.[2,7)
答案
已知二次函数f(x)=x2+ax+1,且f(1)=f(3),则a=()
A.-4 B.-2 C.2 D.4
答案
热门试题
已知函数f(x)= ax为指数函数,且f(2)=9,则f( 1 )=________
已知函数f(x)=ax3-2x的图像过点(-1,4)则a=()
已知函数f(x)=ax3+bx-2,f(2014)=3,则f(-2014)=().
函数f(x)=4x, x∈{-1, 0, 1},则这个函数的值域是( )。
已知函数f(χ)=ax2+b的图像经过点(1,2),且其反函数f-1(χ)的图像经过点(3,0),则函数f(χ)的解析式是()。
已知函数ƒ(x)=ax2+b的图像经过点(1,2),且其反函数ƒ-1(x)的图像经过点(3,0),则函数ƒ(x)的解析式是( )。
已知函数y=x2+ax+a的对称轴为x=-1/2,则a等于则()。
设a<0,则当满足条件()时,函数f(x)=ax3+3ax2+8为增函数。
已知二次函数y=x2+ax+1在区间[1,+∞)上为递增函数,则实数a的取值范围是( )
函数f(x)=ax3-x在R上是减函数,则( )
函数y=(1/3)|x|(x∈R)的值域为()。
已知f(x)=ax2+b的图像经过点(1,2)且其反函数f-1(x)图像经过点(3,0),则函数f(x)的解析式是()。
已知随机变量X~N(2,22),且Y=aX+b~N(0,1),则( )。
已知函数f(x)=x2+ax+2在区间(-∞,1]内单调递减,则实数a的取值范围是()
已知x1,x2是方程x2-ax-1=0的两个实根,则x12x22=
函数f(x)=-cosx+3的值域是()
设函数f(x)=3x3+ax+7在x=1处取得极值,则a=()
当x∈R时,函数y=2sinx+1的值域为[-1,3]。()
若二次函数y=ax2+2ax(a≠0)过p(1,4),则这个函数必过点()
函数y=5x+3的值域是().



 使用微信扫一扫登录
使用微信扫一扫登录