相关试题
换一换


函数y=sin2x与y=tanx的公共周期为()
A.π B.2π C.3π D.4π
答案
函数f(x)=tan2x的周期等于()
A.π/4 B.π/2 C.π D.2π
答案
已知函数f(x)=sinx+2.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的最大值.
答案
函数y=sin2x的周期为()。
答案
若周期函数f(x)的周期为2π,且f(x-π)=-f(x),则f(x)的傅立叶系数。
答案
常微分方程2y2 sinxcosxdx+(2ysin2 x+3y2)dy = 0的通解是( )
A.2y2sinxcosx+(2ysin2 x+3y2)+C B.2y2 sinxcosx+(2ysin2 x+3y2)=C C.y2 sin2 x+y3 +C D.y2 sin2 x+ y3=C
答案
函数y=sin2x的最小正周期是()
A.6π B.2π C.π D.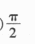
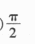
答案
函数y=sin2x的最小正周期是
A.6π B.2π C.π D.π/2
答案
函数y=cos2x的最小正周期是()
A.6π B.4π C.2π D.π
答案
函数y=sin 2x的最小正周期是().
A.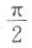 B.π C.2π D.4π
B.π C.2π D.4π
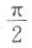 B.π C.2π D.4π
B.π C.2π D.4π 答案
热门试题
函数y=cos2x的最小正周期是()。
函数y=sinx/2sin(π/2-x/2)的最小正周期是()。
函数y=5cos2x一3sin2x的最小正周期为()。
函数y=2x的图像与函数x=log2y的图像( )
设函数Y—sin2xcos2x的最小正周期是 ( )
函数y=2sin6x的最小正周期为()。
函数y=2sin6x的最小正周期为 ( )
函数y=tan(2x+π/4)的最小正周期为()。
函数y=sin2x·tanx的最小正周期是( )
已知函数f(x)=lg(x+1)。 (1)若0f(1-2x)-f(x)1,求x的取值范围; (2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),求函数Y=g(x)(x∈[1,2])的反函数。
已知函数f(x)=lg(x+1)。 (1)若0<f(1-2x)-f(x)<1,求x的取值范围; (2)若g(x)9;g 2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),求函数y-=g(x)x∈[1,2])的反函数。
序列的频谱函数X(e^jw)是w的离散函数,且以2π为周期()
设f(x)是以2π为周期的周期函数,在[-π,π]上的表达式为f(x)=cos(x/2),则f(x)的傅里叶级数为( ).
函数y=tan2x+cosx是一个非奇非偶的周期函数。()
函数y=5cos2x-3sin2x的最小正周期为()。
设f(x)为周期为4的可导奇函数,且f′(x)=2(x-1),x∈[0,2],则f(7)=
设f(x)是周期为4的可导奇函数,且f"(x)=2(x-1),x∈[0,2],则f(7)=________.
设f(x)是以2π为周期的周期函数,在[-π,π)上的表达式为f(x)=x,则f(x)的傅里叶级数为( ).
设f(x)是以2π为周期的周期函数,它在[-π,π)上的表达式为f(x)=|x|,则f(x)的傅里叶级数为( ).
设f(x)是(-∞,+∞)内以4为周期的周期函数,且f(2)=4,则f(6)=



 使用微信扫一扫登录
使用微信扫一扫登录