设f(x)的定义域为所有非零实数之全体,对任何非零实数x、y,f(xy)=f(x)+f(y),且f′(1)存在.
(1)f(x)还有哪些点的导数存在?
(2)求f(x).
查看答案
相关试题
换一换


设f(x)的定义域为所有非零实数之全体,对任何非零实数x、y,f(xy)=f(x)+f(y),且f′(1)存在.(1)f(x)还有哪些点的导数存在?(2)求f(x).
答案
函数y=log2(x-1)的定义域为全体实数。()
答案
函数f(x)的定义域为全体实数,且是以5为周期的奇函数,f(-2)=1,则f(12)等于()。
A.1 B.-1 C.5 D.-5
答案
若实值函数F定义域为全体实数,且满足任意x,y:f(z+3)=f(x)f(y)。此时,若f(8)=4,则有f(2)=()
A.0 B.#$IMG0$# C.#$IMG1$# D.2
答案
“群众是‘零’,杰出人物是‘零’前的非零实数,”这种观点是()
A.肯定了人民群众是社会变革的决定力量 B.夸大杰出人物作用.否定人民群众创造历史 C.告诫杰出人物一定要相信群众.依靠群众 D.正确反映了两者在社会发展中的作用
答案
黎曼Zate函数非平凡零点的实数部份是()
A.0 B.41641 C.41643 D.1
答案
用exp(x)表示以自然对数为底x次幂,函数h(x)=1/(1+exp(-x)),在x的定义域(即实数域)内取值范围(即值域)是()
A.在0,1区间 B.在-1,1之间 C.在整个实数域 D.无法判断
答案
对满足a>b的任意两个非零实数,下列不等式成立的是()。
A.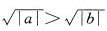 B.
B. C.
C.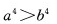 D.
D.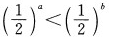
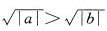 B.
B. C.
C.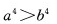 D.
D.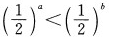
答案
对满足a>b的任意两个非零实数,下列不等式成立的是()
A.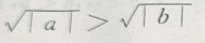 B.
B.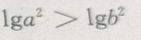 C.
C. D.
D.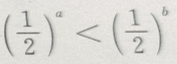
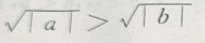 B.
B.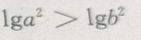 C.
C. D.
D.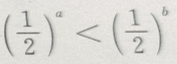
答案
设函数f(x)的定义域为(0,1],则f(sinx)的定义域为()
答案
热门试题
设X为连续型随机变量,对任何实数a,都有P{X=a}=0。()
设函数y=f(ex-1)的定义域为[0,1],则f(x)的定义域是()
设函数y=f(x)的定义域为(1,2],则f(ax)(a<0)的定义域是()
设f(x)=arcsinx,g(x)=lnx,则f[g(x)]的定义域为()
设f(x)=sinx,f[φ(x)]=1-x2,则φ(x)=____,φ(x)的定义域为____。
x^3-1在实数域上有几个根
x^3-1在实数域上有几个根()
若函数ƒ(x)的定义域为[0,1],则ƒ(cosx)的定义域为()。
已知f(x)的定义域为[1,2],则f(2x+3)的定义域为()。
函数f(x)的定义域是[0,1],则函数f(2x)的定义域是().
已知函数f(x)的定义域为[0,1],求函数f(x+a)+f(x-a)(a>0)的定义域.
若函数f(x+1)的定义域是[-1,1],则函数f(x)的定义域是().
已知函数f(x)的定义域是[3,5],求函数f(4x-3)的定义域.
对任意实数x,都有( )。
在实数域R中,x^4-4有几个根()
若函数y=f(x)的定义域是[-1,1],那么f(2x-1)的定义域是()。
已知函数f(x)的定义域为[0,4],则函数φ(x)=f(x+1)+f(x-1)的定义域为____。
函数f(x)=ln x的定义域是()
设x为非零,则下列描述错误的是()
设x为非零,则下列描述错误的是()



 使用微信扫一扫登录
使用微信扫一扫登录