2023年成考高起点每日一练《数学(理)》9月29日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1545
试卷答案:有
试卷介绍: 2023年成考高起点每日一练《数学(理)》9月29日专为备考2023年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 设A、B、C是三个随机事件,用A、B、C的运算关系()表示事件:B、C都发生,而A不发生
A
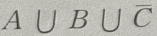
B
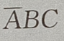
C
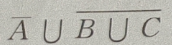
D
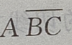
-
2. 若tanα=3,则

A-2
B
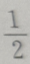
C2
D-4
-
3.
 展开式中,末3项的系数(a,x 均未知) 之和为()
展开式中,末3项的系数(a,x 均未知) 之和为()
A22
B12
C10
D-10
-
4. 若甲:x>1,乙:
 则
则
A甲是乙的必要条件,但不是乙的充分条件
B甲是乙的充分必要条件
C甲不是乙的充分条件,也不是乙的必要条件
D甲是乙的充分条件,但不是乙的必要条件
-
1. 已知直线l的斜率为1,l过抛物线C:
 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|.
-
2. 某工厂每月生产x台游戏机的收入为R(x)=
 +130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
+130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
-
3. 在正四棱柱ABCD-A'B'C'D'中,
 (Ⅰ)写出向量
(Ⅰ)写出向量 关于基底{a,b,c}的分解式
(Ⅱ)求证:
关于基底{a,b,c}的分解式
(Ⅱ)求证: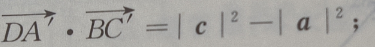 (Ⅲ)求证:
(Ⅲ)求证: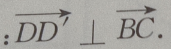
-
4. 已知数列
 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。
-
1. 函数
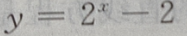 的图像与坐标轴的交点共有()
的图像与坐标轴的交点共有()
-
2. 函数
 的定义域是()
的定义域是()
相关试卷
-
2022年成考高起点每日一练《数学(理)》11月16日1898人做过
-
2022年成考高起点每日一练《数学(理)》11月17日1037人做过
-
2022年成考高起点每日一练《数学(理)》11月18日528人做过
-
2022年成考高起点每日一练《数学(理)》11月19日1716人做过
-
2022年成考高起点每日一练《数学(理)》11月20日1493人做过
-
2022年成考高起点每日一练《数学(理)》11月21日939人做过
-
2022年成考高起点每日一练《数学(理)》11月22日1913人做过
-
2022年成考高起点每日一练《数学(理)》11月23日302人做过
-
2022年成考高起点每日一练《数学(理)》11月24日1434人做过
-
2022年成考高起点每日一练《数学(理)》11月25日183人做过
相关题库