2022年成考高起点每日一练《数学(理)》11月23日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:302
试卷答案:有
试卷介绍: 2022年成考高起点每日一练《数学(理)》11月23日专为备考2022年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 直线3x-4y-9=0与圆
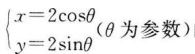 的位置关系是()。
的位置关系是()。A相交但直线不过圆心
B相交但直线通过圆心
C相切
D相离
-
2. 设甲:b=0;乙:函数y=kx+b的图像经过坐标原点,则()
A甲是乙的充分条件但不是必要条件
B甲是乙的充要条件
C甲是乙的必要条件但不是充分条件
D甲既不是乙的充分条件也不是乙的必要条件
-
3. 函数y=2x的图像与直线x+3=0的交点坐标为()。
A
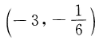
B
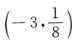
C
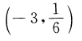
D
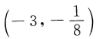
-
4. 已知全集U=R,A={x|x≥1},B={x|-1<x≤2},则
 A∪B=()。
A∪B=()。A{x|x≤2)
B{x|x<2}
C{|x|-1
D{|x|-1
-
1. 建筑一个容积为8000m3,深为6m的长方体蓄水池,池壁每m2的造价为15元,池底每m2的造价为30元。(Ⅰ)把总造价y(元)表示为长x(m)的函数;
(Ⅱ)求函数的定义域。
-
2. 已知{an}是等差数列,且a2=-2,a4=-1. (Ⅰ)求{an}的通项公式; (Ⅱ)求{an}的前n项和Sn.
-
3. 设直线y=x+1是曲线y=x3+3x2+4x+a的切线,求切点坐标和a的值.
-
4.

-
1.
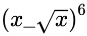 的展开式中,含x4项的系数是().
的展开式中,含x4项的系数是().
-
2. 已知数列{an}的前n项和Sn=2n+1,则a2=()。
相关试卷
-
2025年成考高起点每日一练《数学(理)》1月4日1267人做过
-
2025年成考高起点每日一练《数学(理)》1月5日1988人做过
-
2025年成考高起点每日一练《数学(理)》1月6日1416人做过
-
2025年成考高起点每日一练《数学(理)》1月7日714人做过
-
2025年成考高起点每日一练《数学(理)》1月8日828人做过
-
2025年成考高起点每日一练《数学(理)》1月9日413人做过
-
2025年成考高起点每日一练《数学(理)》1月10日629人做过
-
2025年成考高起点每日一练《数学(理)》1月11日585人做过
-
2025年成考高起点每日一练《数学(理)》1月12日1355人做过
-
2010年成考高起点理科数学真题卷1321人做过
相关题库