2024年成考高起点每日一练《数学(理)》8月25日

• 1. 圆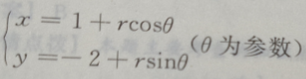的圆心在（）点上  

  A(1,-2)

  B(0,5)

  C(5,5)

  D(0,0)

• 2. 已知棱长为1的正方体ABCD-A’B’C’D’（）。

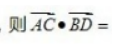  A

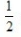
  B0

  C

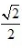
  D

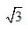
• 3. 设集合M={x∈R|x2=1}，N={x∈R|x3=1}，则M∩N=（）。

  A{1}

  B{-1}

  C{-1，1}

  D

• 4. 方程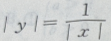的图像是下图中的（）  

  A

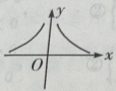
  B

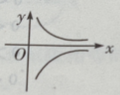
  C

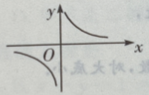
  D

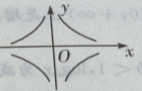
• 1. 求（1+tan10°）（1+tan35°）的值。  

• 2. 设函数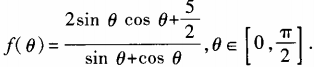（1）求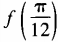；（2）求函数f（θ）最小值。

• 3. 在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量和关于基底{a,b,c}的分解式; （Ⅱ）求证： （Ⅲ）求证：  

• 4. 求下列函数的定义域： （1）
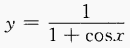
  （2）
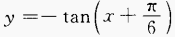
  （3）  

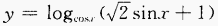
• 1. 若tanα-cotα=1，则=______。

• 2. 若平面向量a=(x,1),b=(1,-2),且a//b,则x=（）