2024年成考高起点每日一练《数学(理)》11月4日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:985
试卷答案:有
试卷介绍: 2024年成考高起点每日一练《数学(理)》11月4日专为备考2024年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 分别和两条异面直线AB、CD同时相交的两条直线AC、BD()。
A相交
B平行
C是异面直线
D垂直
-
2. 已知
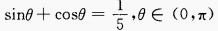 ,则cotθ的值是()。
,则cotθ的值是()。A

B
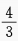
C
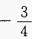
D
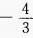
-
3. 在△ABC中,c-acosB=()。
AbcosA
BacosC
CbcosB
DccosA
-
4. 若tan(π-α)>0,且cosα>0,则α的终边在()。
A第一象限
B第二象限
C第三象限
D第四象限
-
1. cos20°cos40°cos80°的值。
-
2. 设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
-
3. 求将抛物线y=x2-2x-3平移到顶点与坐标原点重合时的函数解析式。
-
4. 已知数列{an}中,a1=2,
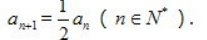 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
-
1. 曲线y=在点(1,1)处的切线方程是______。
-
2. 九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。
相关试卷
-
2024年成考高起点每日一练《数学(理)》3月13日714人做过
-
2024年成考高起点每日一练《数学(理)》3月14日1369人做过
-
2024年成考高起点每日一练《数学(理)》3月15日1050人做过
-
2024年成考高起点每日一练《数学(理)》3月16日516人做过
-
2024年成考高起点每日一练《数学(理)》3月17日347人做过
-
2024年成考高起点每日一练《数学(理)》3月18日1703人做过
-
2024年成考高起点每日一练《数学(理)》3月19日1942人做过
-
2024年成考高起点每日一练《数学(理)》3月20日755人做过
-
2024年成考高起点每日一练《数学(理)》3月21日1463人做过
-
2024年成考高起点每日一练《数学(理)》3月22日1811人做过
相关题库