2024年高职单招每日一练《数学(中职)》11月26日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1494
试卷答案:有
试卷介绍: 2024年高职单招每日一练《数学(中职)》11月26日专为备考2024年数学(中职)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 设△ABC的内角A,B,C的对边分别为a,b,c,若a=2,c=
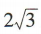 ,cosA=
,cosA=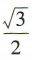 ,则b=()
,则b=()A2
B2或4
C4
D
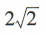
-
2. 李老师随机选取了100名学生某次数学测试的成绩,并分组为[65,70),[70,75),[75,80),[80,85),[85,90),[90,95],绘制了频率分布直方图如图所示,则成绩在区间[70,85)内的学生有()

A35名
B50名
C60名
D65名
-
3. 已知点A(2,1),B(3,2),则直线AB的倾斜角为()
A30°
B45°
C60°
D135°
-
4. 设向量a=(1,x-1),b=(x+1,3),a与b同向,则x的值为()
A2
B-2
C±2
D
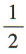
-
1. 已知|a|=|b|=1,a与b的夹角为60°,则(a-2b)·a=()
-
2. 圆x2+y2-2x=0的圆心到直线2x+y-1=0的距离为()
-
3. 已知正四棱锥的底面边长为4,侧棱长为3,则该四棱锥的侧面积为()
-
4. 若
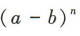 的二项展开式中系数最大的项只有第7项,则n的值为()
的二项展开式中系数最大的项只有第7项,则n的值为()
-
1. 已知点A(-3,0),B(1,0). (1)求以线段 AB 为直径的圆的方程:(2)求过点A,B,且半径为
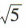 的圆的方程.
的圆的方程.
-
2. 已知α为第二象限角,
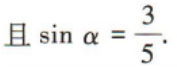 (1)求tanα的值;
(2)求
(1)求tanα的值;
(2)求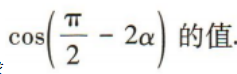
相关试卷
-
2024年高职单招每日一练《数学(中职)》12月15日392人做过
-
2024年高职单招每日一练《数学(中职)》12月16日1683人做过
-
2024年高职单招每日一练《数学(中职)》12月17日1887人做过
-
2024年高职单招每日一练《数学(中职)》12月18日499人做过
-
2024年高职单招每日一练《数学(中职)》12月19日926人做过
-
2024年高职单招每日一练《数学(中职)》12月20日805人做过
-
2024年高职单招每日一练《数学(中职)》12月21日1978人做过
-
2024年高职单招每日一练《数学(中职)》12月22日1975人做过
-
2024年高职单招每日一练《数学(中职)》12月23日1031人做过
-
2024年高职单招每日一练《数学(中职)》12月24日1088人做过
相关题库