2022年成考高起点每日一练《数学(理)》4月19日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:738
试卷答案:有
试卷介绍: 2022年成考高起点每日一练《数学(理)》4月19日专为备考2022年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 已知直线
 l1与l2的夹角是( )
l1与l2的夹角是( )A45°
B60°
C120°
D150°
-
2. 从点M(x,3)向圆(x+2)2+(y+2)2=1作切线,切线长的最小值等于( )。
A4
B
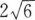
C5
D
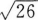
-
3. 命题甲:x2=y2,命题乙:x=y(x,y∈R),甲是乙的( )。
A充分但非必要条件
B必要但非充分条件
C充要条件
D即非充分又非必要条件
-
4. 若a
A
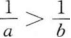
B
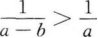
C|a|>|b|
Da2>b2
-
1. 电流强度I随时间t变化的函数关系式是I=Asinωt,设ω=100π(弧度/秒),A=5(安培)。(Ⅰ)求电流强度I变化周期与频率;
(Ⅱ)当t=0,1/200,1/100,3/200,1/50(秒)时,求电流强度I(安培);
(Ⅲ)画出电流强度I随时间t变化的函数的图像。
-
2. 在正四棱柱ABCD-A'B'C'D'中,向量DA=a,向量DC=b,向量DD'=c,

-
3. 设函数f(x)=x3-9/2x2+6x+20。(Ⅰ)求f(x)的单调区间,并说明它在各区间的单调性;
(Ⅱ)求f(x)的极值。
-
4. 建筑一个容积为8000m3,深为6m的长方体蓄水池,池壁每m2的造价为15元,池底每m2的造价为30元。(Ⅰ)把总造价y(元)表示为长x(m)的函数;
(Ⅱ)求函数的定义域。
-
1. lg(tan43°tan45°tan47°)=( )。
-
2. 设离散型随机变量ξ的分布列如下表。那么ξ的期望等于()。

相关试卷
-
2023年成考高起点每日一练《数学(理)》10月28日1619人做过
-
2023年成考高起点每日一练《数学(理)》10月29日1674人做过
-
2023年成考高起点每日一练《数学(理)》10月30日586人做过
-
2023年成考高起点每日一练《数学(理)》10月31日1333人做过
-
2023年成考高起点每日一练《数学(理)》11月1日699人做过
-
2023年成考高起点每日一练《数学(理)》11月2日439人做过
-
2023年成考高起点每日一练《数学(理)》11月3日928人做过
-
2023年成考高起点每日一练《数学(理)》11月4日1444人做过
-
2023年成考高起点每日一练《数学(理)》11月5日1498人做过
-
2023年成考高起点每日一练《数学(理)》11月6日1410人做过
相关题库