2024年成考高起点理科数学全真模拟卷(四)

• 1. 已知函数ƒ(x)=ax²+b的图像经过点(1，2)，且其反函数ƒ^-1(x)的图像经过点(3，0)，则函数ƒ(x)的解析式是(  )。

  A

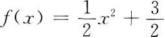
  Bƒ(x)=-x²+3

  Cƒ(x)=3x²+2

  Dƒ(x)=x²+3

• 2. 在△ABC中，已知△ABC的面积=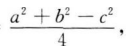，则∠C等于（）。

  A

  B

  C

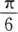
  D

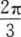
• 3. 设甲：a>b：乙：｜a｜>｜b｜，则(　　)。

  A甲是乙的充分条件

  B甲是乙的必要条件

  C甲是乙的充要条件

  D甲不是乙的充要条件

• 4. 下列函数(　　)是非奇非偶函数。

  Aƒ(x)=x

  Bƒ(x)=x²-2｜x｜-1

  Cƒ(x)=2^｜x｜

  Dƒ(x)=2^x

• 5. 过点(2,-2)且与双曲线x²-2y²=2有公共渐近线的双曲线方程是(  )。

  A

  B

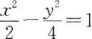
  C

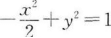
  D

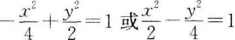
• 6. 在棱长为2的正方体中，M、N分别为棱AA´和BB´的中点，若θ为直线CM与D´N所成的角，则sinθ=(  )。

  A

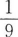
  B

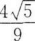
  C

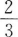
  D

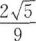
• 7. 甲、乙、丙、丁、戊五个学生排成一排，甲必须排在乙之前的不同排法为（）。

  A

  B

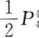
  C

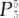
  D

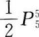
• 8. 下列函数的图像向右平移一个单位长度之后，y=ƒ(x)的图像重合的是（）。

  Ay=ƒ(x+1)

  By=ƒ(x-1)

  Cy=ƒ(x)+1

  Dy=ƒ(x)-1

• 9. 设函数f(x)=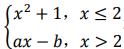在点x=2处可导，则a，b的值依次为（）。

  Aa=1,b=-1

  Ba=-2,b=2

  Ca=4,b=3

  Da=-4,b=3

• 10. 已知集合M={1，-2，3)，N=(-4，5，6，-7)，从这两个集合中各取一个元素作为一个点的直角坐标，其中在第一、二象限内不同的点的个数是（）。

  A18

  B16

  C14

  D10

• 11. 从A、B两个不同的队中选出选手参加比赛，A队有5名选手，B队有4名选手，从A中选出3名选手，B中选出2名选手，则不同的选法有（）。

  A60种

  B72种

  C120种

  D240种

• 12. 已知圆心为C（3，4），且过点B（5，7）的圆的方程为（）。

  A(x+3)²+(y+4)²=13

  B(x-4)²+(y-3)²=13

  C(x+5)²+(y+3)²=13

  D(x-3)²+(y-4)²=13

• 13. 甲：x=1，乙：x²-x=0，则（）.

  A甲是乙的必要不充分条件

  B甲是乙的充分不必要条件

  C甲是乙的充分必要条件

  D甲既不是乙的充分条件也不是乙的必要条件

• 14. 不等式2x²+3＞24x中x的取值范围是（）。

  Ax<1

  Bx>3

  Cx<1或x>3

  Dx≤1或x≥3

• 15. 已知某篮球运动员的投篮命中率为3/5，经过3次投篮之后，至少命中一球的概率为（）。

  A81/125

  B44/125

  C8/125

  D117/125

• 16. 若a

  A

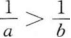
  B

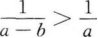
  C｜a｜>｜b｜

  Da2>b2

• 17. 从点M(x，3)向圆(x+2)²+(y+2)²=1作切线，切线长的最小值等于(  )。

  A4

  B

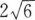
  C5

  D

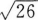
• 1. 设正三角形的一个顶点在原点，且关于x轴对称，另外两个顶点在抛物线y²=2√3上，则此三角形的边长为(  )。

• 2. 将二次函数y=1/3(x-2)²-4的图像先向上平移三个单位，再向左平移五个单位，所得图像对应的二次函数解析式为（）。  

• 3. lg(tan43°tan45°tan47°)=(  )。  

• 4. 已知i，j，k为单位向量且互相垂直，向量a=i+j,b=-i+j-k，则a·b=（）。

• 1. 建筑一个容积为8000m³，深为6m的长方体蓄水池，池壁每m²的造价为15元，池底每m²的造价为30元。(Ⅰ)把总造价y(元)表示为长x(m)的函数；
  (Ⅱ)求函数的定义域。

• 2. 等差数列{a_n}中，a₁=-393，a₂+a₃=-768，{b_n}是等比数列，q∈(0,1)，b1=2，{b_n}的前n项和为20，求：（Ⅰ）求a_n，b_n；
  （Ⅱ）解不等式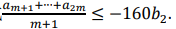

• 3. 设函数f(x)=x³-9/2x²+6x+20。（Ⅰ）求f(x)的单调区间，并说明它在各区间的单调性；
  （Ⅱ）求f(x)的极值。

• 4. 已知P点在以坐标轴为对称轴的椭圆上，点P到两焦点的距离分别为过P点作焦点所在轴的垂线，它恰好过椭圆的一个焦点，求椭圆方程。