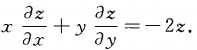2022年统招专升本《高数三》模拟试卷(三)

• 1. 已知函数f（x）在x₀处有二阶导数，且f’（x₀）=0，f”（x₀）=1，,则下列结论正确的是（）。  

  A x=x_{0为f（x）的极小值点}

  Bx=x_{0为f（x）的极大值点}

  C x=x_{0不是f（x）的极值点}

  D（x_{0，f（x0））是曲线y=f（x）的拐点}

• 2. 设函数f（x）满足f”（x）+2xf’（x）=3+e^x，若f’（x₀）=0，则（）。

  Af（x_{0）为f（x）的极小值}

  Bf（x_{0）为f（x）的极大值}

  C（x_{0，f（x0））是曲线y=f（x）的拐点}

  Df（x_{0）不是f（x）的极值，（x0，f（x0））也不是曲线y=f（x）的拐点}

• 3. 下列极限存在的是（）。

  A

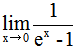
  B

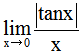
  C

  D

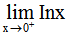
• 4. 下列不是微分方程的是（）。

  Ayy”+y=x²

  Bx^2+y2=cosx

  Cxy’+y=e^x

  D

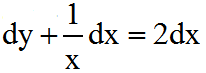
• 5. 若C为任意常数，且F’（x）=f（x），则下列各式成立的是（）。  

  A

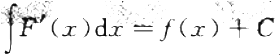
  B

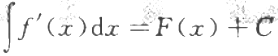
  C

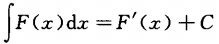
  D

• 1. 若向量组α₁=（1，1+a，0），α₂=（1，2，0），α₃=（0，0，a²+1）线性相关，则a=（）  

• 2. 设y=（2x-1）⁴，则dy|_x=1（）。  

• 3.  

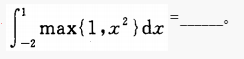
• 4. 函数z=arcsin（x²-2y）+ln（y-1）的定义域为（）

• 5. 设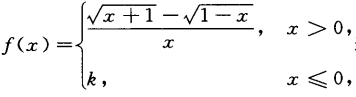若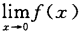存在，则k=（）。

• 1. 设  

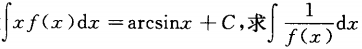
• 2. 求由方程xy=ln（xy）确定的隐函数x=x（y）的导数。  

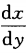• 3. 求定积分。  

• 4. 已知函数y=y（x）是由参数方程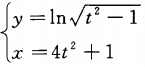，确定的，求曲线y=y（x）在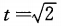处的切线方程。  

• 5. 设函数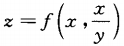，其中f具有一阶连续偏导数，求。  

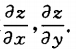• 6. 求定积分  

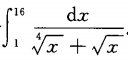
• 7. 设函数y=y（x）由方程ysinx=cos（x-y）所确定，求  

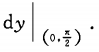
• 8. 求不定积分。  

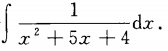• 1. 求由曲线x²+y²=1与y²=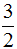x所围成的两个图形中较小的平面图形的面积及其绕x轴旋转一周所生成的旋转体的体积。  

• 2. 欲围成一个面积为150m²的矩形场地，所用材料的造价正面6元/m²，其余三面3元/m²，四面墙的高度相同。试问场地的长和宽各是多少米时，才能使所用的材料费用最低？  

• 1. 已知z=f（x，y）是由e^xyz=sinxyz确定的隐函数，证明：