2023年成考高起点每日一练《数学(理)》1月30日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:336
试卷答案:有
试卷介绍: 2023年成考高起点每日一练《数学(理)》1月30日专为备考2023年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 已知函数f(x)=log2x,则f-1(4)的值为()。
A2
B8
C6
D16
-
2. 过抛物线C:y2=4x的焦点作aT轴的垂线,交C于A,B两点,则|AB|=()。
A2
B4
C
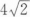
D8
-
3. 函数:y=log2(x+2)的图像向上平移1个单位后,所得图像对应的函数为()。
Ay=log2(x+1)
By=log2(x+3)
Cy=log2(x+2)-1
Dy=log2(x+2)+1
-
4. 不等式|2x-3|≤1的解集为()。
A{x|1≤x≤2}
B{x|x≤-1或≥2}
C{x|1≤x≤3}
D{x|2≤x≤3}
-
1. 已知正六棱锥的高和底的边长都等于a,(Ⅰ)求它的对角面(过不相邻的两条侧棱的截面)的面积、全面积和体积;
(Ⅱ)求它的侧棱和底面所成的角,侧面和底面所成的角。
-
2. 过点(1,-2)且与直线3x+y-1=0垂直的直线方程为.
-
3. 设椭圆的焦点为
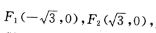 其轴长为4(Ⅰ)求椭圆的方程;(Ⅱ)设直线
其轴长为4(Ⅰ)求椭圆的方程;(Ⅱ)设直线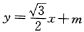 与椭圆有两个不同的交点,其中一个交点的坐标是(0,1),求另一个交点的坐标。
与椭圆有两个不同的交点,其中一个交点的坐标是(0,1),求另一个交点的坐标。
-
4. 某县位于沙漠边缘,到1999年底全县绿化率已达30%.从2000年开始,每年出现这样的局面:原有沙漠面积的16%被栽上树改为绿洲,而同时原有绿地面积的4%又被侵蚀,变为沙漠。(Ⅰ)设全县的面积为1,1999年底绿洲面积为a1=3/10,经过一年绿洲面积为a2,经过n年绿洲面积为an,求证:an+1=4/5an+4/25;
(Ⅱ)问至少经过多少年的绿化,才能使全县的绿洲面积超过60%(年取整数)。
-
1. 若向量a=(2,1,-2),b=(-1,2,2),则cos(a,b)=________
-
2. 已知数列{an}的前n项和Sn=2n+1,则a2=()。
相关试卷
-
2024年成考高起点每日一练《数学(理)》1月30日937人做过
-
2024年成考高起点每日一练《数学(理)》1月31日1582人做过
-
2024年成考高起点每日一练《数学(理)》2月1日1301人做过
-
2024年成考高起点每日一练《数学(理)》2月2日1633人做过
-
2024年成考高起点每日一练《数学(理)》2月3日1254人做过
-
2024年成考高起点每日一练《数学(理)》2月4日115人做过
-
2024年成考高起点每日一练《数学(理)》2月5日1329人做过
-
2024年成考高起点每日一练《数学(理)》2月6日691人做过
-
2024年成考高起点每日一练《数学(理)》2月7日1170人做过
-
2024年成考高起点每日一练《数学(理)》2月8日200人做过
相关题库