2023年成考高起点每日一练《数学(文史)》2月27日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1488
试卷答案:有
试卷介绍: 2023年成考高起点每日一练《数学(文史)》2月27日专为备考2023年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 函数
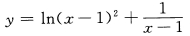 的定义域为
的定义域为A{x|x<-1或x>1}
B{x|x<1或x>1}
C{x|-1
DR
-
2. 某学校为新生开设了4门选修课程,规定每位新生至少要选其中3门,则一位新生不同的选课方案共有 ( )
A7种
B4种
C5种
D6种
-
3. 函数f(x)=1+cosx的最小正周期是()
A
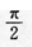
Bπ
C
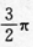
D2π
-
4. 从5位同学中任意选出3位参加公益活动,不同的选法共有 ( )
A5种
B10种
C15种
D20种
-
1. 已知A,B为⊙O上的两点,且AB=
 ∠ABO=30°.求⊙O的半径。
∠ABO=30°.求⊙O的半径。
-
2. 在△ABC中,A=30°,AB=
 ,BC=1.(Ⅰ)求C;(Ⅱ)求△ABC的面积.
,BC=1.(Ⅰ)求C;(Ⅱ)求△ABC的面积.
-
3. 在平面直角坐标系xOy中,已知⊙M的方程为x2+y2-2x+2y-6=0,⊙O经过点M. (Ⅰ)求⊙O的方程; (Ⅱ)证明:直线x-y+2=0与⊙M,⊙O都相切.
-
4. 椭圆的焦点F1(-1,0),F2(1,0),|F1F2|是|PF1|和|PF2|的等差中项。
(Ⅰ)求椭圆方程;
(Ⅱ)若∠F2F1P=120°,求△PF1F2的面积。
-
1. 某中学五个学生的跳高成绩(单位:米)分别为1.68、1.53、1.50、1.72、a(未知数),他们的平均成绩为1.61米,则a=
-
2. 曲线y=x3—2x在点(1,-1)处的切线方程为 .
相关试卷
-
2022年成考高起点每日一练《数学(文史)》5月2日1530人做过
-
2022年成考高起点每日一练《数学(文史)》5月3日792人做过
-
2022年成考高起点每日一练《数学(文史)》5月4日1920人做过
-
2022年成考高起点每日一练《数学(文史)》5月5日1032人做过
-
2022年成考高起点每日一练《数学(文史)》5月6日1197人做过
-
2022年成考高起点每日一练《数学(文史)》5月7日1169人做过
-
2022年成考高起点每日一练《数学(文史)》5月8日854人做过
-
2022年成考高起点每日一练《数学(文史)》5月9日1760人做过
-
2022年成考高起点每日一练《数学(文史)》5月10日1826人做过
-
2022年成考高起点每日一练《数学(文史)》5月11日917人做过
相关题库