一个圆锥底面半径为r,母线长为l,它的侧面积是( )
A. πrl
B. πr²l
C. 1/2πrl
D. 2πr²
查看答案
相关试题
换一换


一个圆锥底面半径为r,母线长为l,它的侧面积是( )
A.πrl B.πr²l C.1/2πrl D.2πr²
答案
已知圆锥的底面半径为√2,其侧面展开图为一个半圆,则该圆锥的母线长为
A.2 B.2√2 C.4 D.4√2
答案
一个圆柱底面半径为r,高为h,它的侧面积是( )
A.2πrh B.πr²h C.πrh D.4πr²
答案
已知圆锥的侧面积是12π平方厘米,底面半径是3厘米,则这个圆锥的母线长是()
A.3cm B.4cm C.5cm D.8cm
答案
已知圆锥底面圆的半径为2,母线长是4,则它的全面积为()
A.4π B.8π C.12π D.16π
答案
已知一个圆锥的母线长为6,侧面积为18π,则此圆锥的体积为()
A.9π B.12π C. D.
D.
 D.
D.
答案
一个圆锥的表面积为S,拆开它的侧面是一个半圆,那么求底面直径为( ).
A.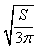 B.
B. C.
C.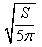 D.
D.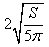
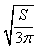 B.
B. C.
C.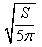 D.
D.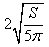
答案
用半径为2cm的半圆围成一个圆锥的侧面,这个圆锥的底面半径为()
A.1cm B.2cm C.πcm D.2πcm
答案
已知圆锥体的母线长为4,侧面积为4π,则它的体积为()
A.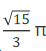 B.
B.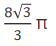 C.
C.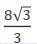 D.
D.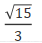
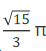 B.
B.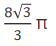 C.
C.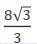 D.
D.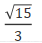
答案
已知圆锥的高与底面圆的半径相等,若底面圆的面积为1,则该圆锥的侧面积是()
答案
热门试题
一个底面半径是10cm的圆锥,如果底面积不变,高增加3cm,它的体积会增加()cm³
若圆锥的表面积为S,且它的侧面展开图是一个半圆,则这个圆锥的底面圆直径为().
已知圆锥的母线长为3,侧面积为3√5π,则该圆锥的高为()
如果一个圆锥的侧面展开图是半圆,那么其母线与底面所成角的大小是 ( )
一个圆柱的底面半径是3厘米,高是5厘米,它的侧面积是()平方厘米
一个圆锥体零件的底面半径为8厘米,高为6厘米。现一刀将该零件切成为2个完全相同的部分,问每个部分的表面积在以下哪个范围内(圆锥侧面积公式:S侧=πRL,L为圆锥母线,π≈3.14)
一个圆柱的侧面展开图是正方形,那么它的侧面积是下底面积的( )倍
一个正三棱柱,底面边长为a,高为h,它的侧面积是( )
圆锥底面的半径为5cm,高为12cm,则圆锥的侧面积为_____cm2。
一个圆柱,如果底面半径和高都扩大到原来的3倍,那么它的侧面积扩大到原来的()倍
已知圆锥的底面半径为2cm,高为1cm,则圆锥的侧面积是14.04平方厘米。()
一个圆柱和一个圆锥的体积相等,底面半径的比是2:1,那么圆柱和圆锥的高的比是()
一个圆柱体和一个圆锥体体积相等,高也相等,那么圆锥体的底面积就是圆柱体底面积的3倍()
一个正四棱锥,底面边长为4cm,高为3cm,它的侧面积是( )
一个圆柱与圆锥的体积相等,圆柱的底面积是圆锥体的底面积的3倍,圆锥体的高与圆柱的高的比为()
一个圆锥的体积是3立方米,底面积是3平方米,它的高是()米
圆柱的轴截面面积等于10,体积为5π,它的母线长和侧面积分别是( )
一个圆柱与圆锥体的体积相等,圆柱的底面积是圆锥体的底面积的倍,圆锥体的高与圆柱的高的比为()
若一个圆柱的母线长等于底面圆的直径,且该圆柱的体积为16π,则该圆柱的母线长为()
一个圆柱的侧面展开图是一个正方形,这个圆柱的底面半径与高的比是()



 使用微信扫一扫登录
使用微信扫一扫登录