相关试题
换一换


|z+3+4i|≤2,则|z|的最大值为()
A.3 B.7 C.9 D.5
答案
求函数u=x2+y2+z2在约束条件z=x2+y2和x+y+z=4下的最大值和最小值。
答案
设复数z满足(1+i)z=2i ,则z=( )
A.−1+i B.−1−i C.1+i D.1−i
答案
判断下列命题是否正确。
(1)若z∈C,则z2≥0;
(2)若z1,z2∈C,且z1-z2>0,则z1>z2;
(3)若a>b,则a i>b i。
答案
判断下列命题是否正确。(1)若z∈C,则z2≥0;(2)若z1,z2∈C,且z1-z2>0,则z1>z2;(3)若a>b,则a+i>b+i
答案
若复数z1=1+i,z2=3-i,则z1·z2=( )
A.4+2 i B.2+ i C.2+2 i D.3
答案
若复数z满足(1+i)z=2 (i为虚数单位),则z=( )
A.1−i B.i C.1+i D.2i
答案
已知(1-i)²z=3+2i,则z=
答案
设u=2xy-z^2,则u在点(2,-1,1)处的方向导数的最大值为( )。
A.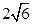 B.4 C.(-2,-4,-2) D.6
B.4 C.(-2,-4,-2) D.6
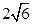 B.4 C.(-2,-4,-2) D.6
B.4 C.(-2,-4,-2) D.6 答案
判断下列命题是否正确。 (1)若z∈C,则z2≥0; (2)若z1,z2∈C,且z1-z2>0,则z1>z2; (3)若a>b,则a+i>b+i。
答案
热门试题
判断下列命题是否正确。(1)若z∈C,则z2≥0;(2)若z1,z2∈C,且z1-z2>0,则z1>z2;(3)若a>b,则a+i>b+i
已知z1= 1+i,z2= 2+ 3i,则z1+Z2=______
z1=4+2i,z2=5-i,则( )
在复平面内,复数z满足(1-i)z =2,则z= ()
若复数z1=2+3i,z2=-4-5i,则z1+z2=()
设a,b为实数,函数z=2+ax^2+by^2在点(3,4)处的方向导数中,沿方向l=-3i-4j的方向导数最大,最大值为10. (Ⅰ)求a,b; (Ⅱ)求曲面z=2+ax^2+by^2(z≥0)的面积.
已知i为虚数单位,(2+i)z=1+2i ,则Z的共轭复数( )
复数z满足(1+i)z=1-i,则|Z|=()。
若复数z满足(1−i) z=3+i,则z=( )
设z=x+y-2x2-2y2+1,求z在点(1,1)处的梯度,并求函数z在该点的方向导数的最大值和最小值.
类比高等数学可以得到φ(z)在圆盘|z|≤r这个有界闭集上没有最大值,也没有最小值()
类比高等数学可以得到φ(z)在圆盘|z|≤r这个有界闭集上没有最大值,也没有最小值。
int x=2;z=++x+1; 则z的值为【1】.
intx=y=4,z=2;x=y==z;则x的值为
已知复数z=(1−i)(1+2i),其中i为虚数单位,则z的实部为( )
设有语句:char x=6,y=10;int z; z=(x^y)<<2; 则z的值是:
intx=2,y=2,z=0;则表达式x==y>z的值为
intx=4,y=z=2;x=x==(y=z);则x的值为
已知int x,y,z; x=4,y=z=2;x=x==(y=z); 则x的值为_____.
若z1=2−3i,z2=1+4i,z3=−1+2i,计算z1+2z2−3z3.



 使用微信扫一扫登录
使用微信扫一扫登录