m x→0
查看答案
相关试题
换一换


0级平板的表面接触斑点应达到25mx2()
A.20~23点 B.23~25点 C.大于或等于25点 D.8~12点
答案
已知直线x-y-2=0与直线mx+y=0垂直,则m的值是( )。
A.- 2 B.-1 C.1 D.2
答案
若直线mx+y-1=0与直线4x+2y+1=0平行,则m=()
A.-1 B.0 C.2 D.1
答案
若直线mx+y-1=0与直线4x+2y+1=0平行,则m=()
A.-1 B.0 C.2 D.1
答案
如果直线3x-y=0与直线mx+y-1=0平行,那么m的值为()
A.-3 B.-1/3 C.1/3 D.3
答案
如果直线3x-y=0与直线mx+y-1=0平行,那么m的值为( )
A.-3 B.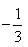 C.
C.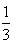 D.3
D.3
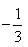 C.
C.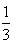 D.3
D.3 答案
如果直线3x+y-20=0与2mx+4y+20=0垂直,则m的值是( )。
A.1 B. C.
C.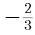 D.-2
D.-2
 C.
C.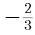 D.-2
D.-2 答案
若直线mx+4y-2=0与直线2x-5y-12=0垂直,则实数m的取值为()
A.-2 B.2 C.-10 D.10
答案
三条直线x-y=0,x+y-1=0,mx+y+3=0不能构成三角形,则m取值的集合为________.
答案
空间一般力系有∑X=0,∑Y=0,∑Z=0,∑Mx=0,∑My=0,∑Mz=0六个平衡方程,若有一个在xy平面内的平面一般力系,则其平衡方程是()。
A.∑X=0,∑Y=0,∑Mx=0 B.∑X=0,∑Y=0,∑My=0 C.∑X=0,∑Y=0,∑Mz=0 D.∑X=0,∑Z=0,∑Mz=0
答案
热门试题
已知两点O(0,0),A(4.-1)到直线mx+m2y+6=0距离相等,则实数m可取的不同值共有()
对于常数m,n,“mn>0”是“方程mx2+ny2=1表示的曲线是椭圆”的( )。
对于常数m,n,mn0是方程mx2+ny2=1的曲线是椭圆的( )
直线mx-y+n=0过点(2,2),则4m+2n的最小值为( ).
已知A(2,-3),B(3,-2),直线l的方程为mx+y+1=0,若直线l//AB,则m=()
mooc 现有如下谓词逻辑推理:"x(Mx→Px),"x(Sx→Mx)├$x(Sx∧Mx)。下列说法正确的是:
设一空间力F在x轴上的投影Fx=0,对x轴之矩Mx(F)=0,那么该力与x轴的关系为( )。
设一空间力F在x轴上的投影Fx=0,对x轴之矩Mx(F)=0,那么该力与x轴的位置关系为()
已知直线l1:mx+y+3=0,l2:2x-y+3=0.若l1⊥l2,则m=()
若方程x2+y2+mx-4y+5=0表示圆,则实数m的取值范围是()
砂的粗细程度用细度模数(MX)表示,细砂的MX值范围为( )。
砂的粗细程度用细度模数(Mx)表示,细砂的Mx值范围为( )。
砂的粗细程度用细度模数(Mx)表示,细砂的Mx值范围为( )。
直线l:mx-y+1-m=0与圆C:x2+(y-1)2=5的位置关系是().
砂的粗细程度用细度模数(MX)表示,粗砂的MX值范围为( )。
砂的粗细程度用细度模数(MX)表示,粗砂的MX值范围为( )。
在配制混凝土时,适用的砂由Mx=2.6变为Mx=3.5时,其砂率( ; ;)。 ;
砂的粗细程度用细度模数(Mx)表示.粗砂的Mx值范围为()
砂的粗细程度用细度模数(MX)表示。中砂的MX值范围为( )。
砂的粗细程度用细度模数(Mx)表示,粗砂的Mx值范围为( )。



 使用微信扫一扫登录
使用微信扫一扫登录