编一个程序,输入a,b,c的值,求出一元二次方程a*x*x+b*x+c=0的二个实数根。计算二个实数根必须使用Math类中的Sqrt()方法,计算指定数的开方。计算二个实数根,可以用公式(-b+Math.Sqrt(b*b-4*a*c))/(2*a)和(-b-Math.Sqrt(b*b-4*a*c))/(2*a)
查看答案
相关试题
换一换


一元二次方程为初中阶段重要的方程形式,一元二次方程的解法多样,下列属于一元二次方程解法的有()
A.配方法 B.公式法 C.因式分解法 D.代入消元法
答案
一元二次方程的实根()
A.至少一个 B.最多二个 C.没有 D.只有一个
答案
下列方程是一元二次方程的是()
A.x²-y-1=1 B.x²+2x-3=0 C.x²+ =3 D.x-5y=6
答案
一元二次方程中的“元”指的是什么()
A.未知数 B.常数
答案
一元二次方程中的“元”指的是什么?()
A.加减乘除 B.未知数
答案
第一个提出一元二次方程有求根公式的人是
答案
下列方程中不是一元二次方程的是
答案
下列方程中,属于一元二次方程的是()
A. B.2y+x2=1 C.x2﹣2=0
答案
下列方程中,是一元二次方程的是()
A.x+3=0 B.x2-3y=0 C.(x+3)(x-3)=1 D.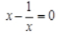
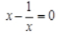
答案
下列方程中,关于x的一元二次方程是()
A.x2-x(x+3)=0 B.ax2+bx+c=0 C.x2-2x+3=0 D.x2-2y-1=0
答案
热门试题
根据代数基本定理,一个一元二次方程式通常有几个根?()
中国大学MOOC: 求一元二次方程的根
一元二次方程仅可以用代数法解决。
托马斯·卡莱尔首次利用()解出了一元二次方程。
中国大学MOOC: 编程计算一元二次方程的根。
下列一元二次方程有两不等实数根的是()
用C语言编写的求解一元二次方程的程序是系统软件。
求解一元二次方程的核心思想是降次,将一元二次方程转化为一元一次方程。《义务教育数学课程标准(2011年版)》要求:理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程。 请完成下列任务: (1)请至少说出3种课标要求中解一元二次方程的方法所包含的降次过程;(2)设计公式法解一元二次方程的主要教学过程; (3)运用因式分解法计算一元二次方程比较简单,初中常用的因式分解法是十字相乘法, 请写出十字相乘法的主要步骤。
数学老师在课堂上讲解一元二次方程的时候,小毛同学提出老师讲错了一元二次方程的解题方法,这时该老师最恰当的做法是()
元二次方程的定 义:只含有一个未知数的整式方程,未知数的最高次数为2,可将方程式化为一般形式ax二次方+bx+c=0(a≠0)。则下列关于x的方程是一元二次方程的是()
针对一元二次方程概念与解法的一节复习课,教学目标如下:① 进一步了解一元二次方程的概念;② 进一步理解一元二次方程的多种解法;③ 会运用判别式判断一元二次方程根的情况;④ 通过对相关问题的讨论,在理解相关知识的同时,体会数学思想方法,积累数学活动经验。问题:根据上述教学目标,完成下列任务:(1)为了落实上述教学目标①②,请设计一个教学片段,并说明设计意图;(2)配方法是解一元二次方程的通性通法,请
一元二次方程的求根公式体现了数学美中的哪个境界?
已知一元二次方程ax2-5x+6=0的一个根是2,则a的值是()
针对一元二次方程概念与解法的一节复习课,教学目标如下:①进一步了解一元二次方程的概念;②进一步理解一元二次方程的多种解法(配方法、公式法、因式分解法等);③会运用判别式判断一元二次方程根的情况:④通过对相关问题的讨论,在理解相关知识的同时,体会数学思想方法,积累数学活动经验。问题:根据上述教学目标,完成下列任务:(1)为了落实上述教学目标①、②,请设计一个教学片段,并说明设计意图;(2)配方法是解一元二次方程的通性通法,请设计问题串,以帮助学生进一步理解配方法在解一元二次方程中的作用。
针对一元二次方程概念与解法的一节复习课,教学目标如下:① 进一步了解一元二次方程的概念;② 进一步理解一元二次方程的多种解法(配方法、公式法、因式分解法等);③ 会运用判别式判断一元二次方程根的情况;④ 通过对相关问题的讨论,在理解相关知识的同时,体会数学思想方法,积累数学活动经验。问题:根据上述教学目标,完成下列任务:(1)为了落实上述教学目标①②,请设计一个教学片段,并说明设计意图;(18分)(2)配方法是解一元二次方程的通性通法,请设计问题串,以帮助学生进一步理解配方法在解一元二次方程中的作用。(12分)
已知α,β是一元二次方程x2+4x-5=0的两个根,则α+β的值为( )
针对“一元二次议程”起始课的教学,两位老师给出了如下教学设计片段:
【教师甲】
设置问题:请同学们根据下列问题,只列出含未知数x的方程:
(1)一个正方形的面积为2,求正方形的边长x。
(2)长度为1的线段AB有一点C,且满足AC/AB=BC/AC,求线段AC的长x。
预设:学生会分别列出两个方程。
教师要求学生分别整理成方程左侧降幂排列,右侧为零的形式,然后引导学生完成下面两件事:对比”一元一次方程“的定义,为这类议程定义一个名称——一元二次方程。再请学生自行写出几个不同的一元二次议程,并提炼出一元二次方程的一般表达式。
【教师乙】
上课开始。提问:什么是“一元一次方程”?请你根据“一元一次方程”的定义,给出“一元二次方程”的定义,并举出几个“一元二次方程”的例子。在学生举例的基础上,提炼出“一元二次方程”的一般表达式。
请完成下列任务:
(1)请分析两位老师引入“一元二次方程”概念设计方案的各自的特点。
(2)在教学中,当引入一个新的数学概念之后,往往通过例题、习题加深对概念的理解。请针对“一元二次方程”概念,设计不同难度的两道例题和两道习题,以加深学生对“一元二次方程”概念的理解。
列举义务教育阶段一元二次方程的三种主要解法.
一元二次方程2x^2-7x+8=0的一次项是()
把一元二次方程(x+2)(x-3)=4化成一般形式,得()



 使用微信扫一扫登录
使用微信扫一扫登录