设a>0,b>0,证明:ab+ba>1
查看答案
相关试题
换一换


设a>0,b>0,证明:ab+ba>1
答案
设集合A={0,1},B={0,1,2},则A∩B=()。
A.{1,2} B.{0,2} C.{0,1} D.{0,1,2}
答案
设集合A={0,1},B={0,1,2},则A∩B=
A.{0,1} B.{0,2} C.{1,2} D.{0,1,2}
答案
设集合A={0,1},B={0,1,2},则A∩B=()
A.{1,2} B.{0,2} C.{0,1} D.{0,1,2}
答案
设0<P(A)<1,0<P(B)<1,P(A|B)+P(A(_)|B(_))=1,则( )。
A.事件A与B互不相容 B.事件A与B相互独立 C.事件A与B相互对立 D.事件A与B互不独立
答案
设0<a<b<1,则()
A.loga2 b2 B.loga2>logb2 C.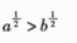 D.
D.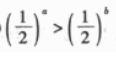
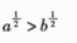 D.
D.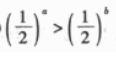
答案
设0<a<b<1,则()。
A.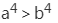 B.
B.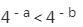 C.
C. D.
D.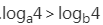
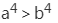 B.
B.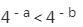 C.
C. D.
D.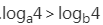
答案
设P(A)>0,P(B)>0,证明A、B互不相容与A、B相互独立不能同时成立.
答案
设函数f(x)在[a,b]上连续,满足f([a,b])∈[a,b]。证明:存在x0,∈[a,b],使得f(x0)=x0。
答案
设集合A=(0,+∞),B=(-1,1),则A∩B=().
A.(0,1) B.(-1,-∞) C.(-1,1) D.(0,+∞)
答案
热门试题
设f(x)在[0,c]上有定义,f′(x)存在且单调递减,f(0)=0,证明:对于0≤a≤b≤a+b≤c,恒有f(a+b)≤f(a)+f(b).
设集合A={-1,0,1,2},B={0,2,3},则AUB=()
设集合A={-1,0,1,2},B={0,2,3},则AUB=()
设P(B)>0,P(A│B)=1,则必有:()
设a、b为实数,0<a<b,证明在开区间(a,b)中存在有理数(提示取1/2<b一a)。
设f(x)在[0,1]上二阶可导,且f(0)=f(1)=0。证明:∃ξ∈(0,1)使(ξ-1)3f″(ξ)+2f′(ξ)=0。
设f(x),f′(x)在[a,b]上连续,f″(x)在(a,b)内存在,f(a)=f(b)=0,且存在c∈(a,b)使f(c)>0。证明:必∃ξ∈(a,b)使f″(ξ)<0。
设0
设0
设A、B是两个随机事件,且0<P(A)<1,P(B)>0,P(B|A)=P(B|A(_)),则必有( )。
已知a>b>0,c<d<0.证明:
(1)a-c>b-c;
(2)ac<bd.
设集合A={-1,0,1,2},B={x l x2-4=0},那么AUB=()
设函数f(x)在[0,1]上二阶可导,且f(0)=f(1)=0,证明:必∃ξ∈(0,1)使ξ2f″(ξ)+4ξf′(ξ)+2f(ξ)=0。
设集合A={x|x²=1},B={x|x(x-1)=0},则A∪B=()
设a<0<b,则( ).
设n为正整数,0<x<1,证明:xn(1-x)<1/(ne)。
证明:(a+b)ea+b≤ae2a+be2b,(a>0,b>0)。
设A、B相互独立,P(A)=0.6,0<P(B)<1,则P(A(_)|B(_))=____。
设A、B为随机事件,且P(B)>0,P(A|B)=1,则必有( )。
设a>0,b≠0为常数且,则(a,b)的取值为()



 使用微信扫一扫登录
使用微信扫一扫登录