三个质量均为2 kg的质点,位于边长为0.2 m的等边三角形的三个顶点上。此系统对通过三角形中心和一个顶点的轴的转动惯量为_____kg·m2。(不计三角形的质量)
查看答案
相关试题
换一换


三个质量均为2 kg的质点,位于边长为0.2 m的等边三角形的三个顶点上。此系统对通过三角形中心和一个顶点的轴的转动惯量为_____kg·m2。(不计三角形的质量)
答案
边长为2的等边三角形的面积()
A.3 B. C.
C. D.
D.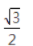
 C.
C. D.
D.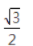
答案
Bonwill论述的等边三角形的三个角居于()。
A.两侧髁状突的中心及眉间点 B.两侧髁状突的中心及下颌中切牙的近中接触点 C.两侧髁状突的中心及上颌中切牙的近中接触点 D.两侧颞下颌关节窝及上颌中切牙的近中接触点 E.两侧颞下颌关节窝及下颌中切牙的近中接触点
答案
Bonwill等边三角
答案
一个等边三角形其中一条边长度为m米,这个三角形的周长是()。
A.m3 B.3m C.无法表示
答案
边长为2的等边三角形的外接圆的面积为()
答案
扁钢、等边三角钢、不等边三角钢的规格以的尺寸表示()
A.A-厚度 B.B-各边宽及厚度 C.C-角度 D.D-边宽
答案
等边三角形的三个内角都是多少度?
答案
邦威尔(Bonwill)等边三角形学说中,三角形的角位于
A.两侧下颌第一磨牙及下颌两中切牙的近中接触区 B.两侧髁状突中心及下颌两中切牙的近中接触区 C.两侧颞下颌关节凹及上颌两中切牙的近中接触区 D.两侧上颌第一磨牙及上颌两中切牙的近中接触区 E.两侧颞下颌关节凹及下颌两中切牙的近中接触区
答案
井网呈等边三角形,注水井按一定的井距布置在等边三角形的三个顶点上,采油井位于三角形的中心,这样的注采方式为()面积井网。
A.点状 B.三点法 C.四点法 D.五点法
答案
热门试题
等边三角形边长减少为原来的50%,面积减少了:
等边三角形有()个锐角。
三个质量均为m的质点,位于边长为a的等边三角形的三个顶点上.此系统 对通过三角形中心并垂直于三角形平面的轴的转动惯量J0=____ma2, 对通过三角形中心且平行于其一边的轴的转动惯量为JA=____ma2, 对通过三角形中心和一个顶点的轴的转动惯量为JB=____ma2.(用整数或小数填空,比如1、2、0.3、0.5)
等边三角形是()。
三角形:等腰三角形:等边三角形()
职责和权限、利益、能力之间遵循等边三角形定理,( )是三角形的三个边,它们是相等的。
△ABC为等边三角形,若DEF为三角形三个边的中点,用ABCDEF六个点中的任意三个作顶点,可有多少种面积不等的三角形( )
井网等边三角形,将注水井按一定的井距布置在等边三角形的3个顶点上,采油井位于三角形的中心,这样的注采方式为( )面积井网。
正等边三角形标志用于()
职责和权限、利益、能力之间的关系遵循等边三角形定理,()是三角形的三个边,它们是相等的。
职责和权限、利益、能力之间的关系遵循等边三角形定理,是三角形的三个边,它们是相等的
△ABC为等边三角形,若DEF为三角形三个边的中点,用ABCDEF六个点中的任意三个作顶点,可有多少种面积不等的三角形?( )
所有的等边三角形都是等腰三角形。()
判断真假:所有等边三角形都是等角三角形
所有的等边三角形都是等腰三角形()
正等边三角形用于警告标志()
职责和权限、利益、能力之间的关系遵循等边三角形定理,这三个相等的边是:
职责和权限、利益和能力之间的关系是遵循等边三角形定理,三个边是指
等边三角形排列的三相输电线路,其相间几何均距为()
案例
下面是两位教师关于《等边三角形》的教学过程
教师甲
教师乙
(1)复习等腰三角形的性质及判定方法。
教师提问、学生思考:边怎样 角怎样 对称性呢
(2)等边三角形性质的教学。
教师提问、学生思考:
①什么样的三角形叫等边三角形
②等边三角形的三个内角都相等吗
③等边三角形是轴对称图形吗
(3>等边三角形判定的教学
师:哪位同学说说我们应从什么角度来考虑等边三角形
的判定方法
生:从角和边来考虑。(教师希望的答案是从边和角来考
虑)
师:那你能说一下等边三角形有怎样的判定方法吗
生:从角来说,我认为三个内角都是600的三角形是等边
三角形(学生的回答出乎老师的预设,打乱了PPT的放
映程序)
师:关于边的研究比较简单,我们还是从边开始探讨吧。
生:好。(学生没有异议,只能跟着老师的要求回答问题,
继续学习)
(1)复习引入
①理解等腰三角形的定义、性质;
②观察生活中的等边三角形,引出课题。
(2)新课教学
①等边三角形有什么性质
(PPT显示)可以从边、角、对称性来考虑
设计活动1:
学生拿出课前准备的等边三角形纸片,认真折叠并
观察,小组合作,互相探讨,一个小组代表发表自己
组的观点.其他小组补充,最后一起归纳总结。
②等边三角形的判定方法有哪些 设计开放性提问
(唧’显示)
你认为怎样才能说明三角形是等边三角形 等腰三
角形怎样变化才能说明是等边三角形
设计活动2:
小组合作,互相探讨,教师操作几何画板,学生也上
台操作几何画板,观察等腰三角形满足什么条件后
成为等边三角形。学生积极主动地参与课堂学习,能
够在折纸操作后很快说出等边三角形的性质和判定
方法.通过操作几何画板形象地展现变化过程。新知
识的获得和掌握很快且水到渠成,最后教师和学生
一起归纳总结。
问题:
请从下列三个方面对甲乙两位教师的教学过程进行评价:
(1)引入的特点;(6分)
(2)教师教的方式;(7分)+
(3)学生学的方式。(7分)



 使用微信扫一扫登录
使用微信扫一扫登录