已知直线x+y-m=0经过点P(-2,1),则m的值为( )。
A. -2
B. -1
C. 1
D. 2
查看答案
相关试题
换一换


已知直线x+y-m=0经过点P(-2,1),则m的值为( )。
A.-2 B.-1 C.1 D.2
答案
已知点P(-2,1)到直线l:3x-4y+m=0的距离为1,则m的值为()
A.-5或-15 B.-5或15 C.5或-15 D.5或15
答案
已知过点 A(m+1,0),B(-5,m)的直线与过点 C(-4,3),D(0,5)的直线平行,则m的值为()
答案
过点P(m,4)和点Q(1,m)的直线与直线x-2y+4=0平行,则m的值为()
答案
已知α的终边经过点P(3m,-4m),若m>0,则sinα =______,cosα =______,tanα=______.
答案
已知两点O(0,0),A(1,0),直线l:x-2y+1=0,P为直线l上一点,则|PO|+|PA|的最小值为().
A.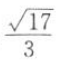 B.
B.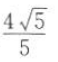 C.
C.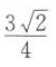 D.
D.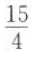
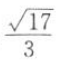 B.
B.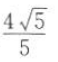 C.
C.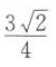 D.
D.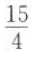
答案
已知直线x-y-2=0与直线mx+y=0垂直,则m的值是( )。
A.- 2 B.-1 C.1 D.2
答案
已知过点P(-2,m)、Q(m,4)的直线斜率为1,则m等于( )
A.1 B.4 C.1或3 D.1或4
答案
已知直线l的方程是kx-y+2+3k=0(k∈R),则直线l必经过点________.
答案
已知两点O(0,0),A(4.-1)到直线mx+m2y+6=0距离相等,则实数m可取的不同值共有()
A.1个 B.2个 C.3个 D.4个
答案
热门试题
已知直线l经过两点M(-2,m),N(m,4)若直线l的倾斜角为45°,则实数m=()
已知三点 A(0,2),B(2,m),C(5,12)在同一条直线上,则实数m的值为()
经过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为()
若过点P(-1,3)和点Q(1,7)的直线l₁与直线l₂:mx+(3m-7)y+5=0平行,则m的值为()
已知点A(1,3)和点B(m,0)的距离为5,则m的值为( )。
已知直线l经过点P(2,1),且与直线5x+2y+3=0的夹角等于45°,求直线l的方程.
已知角α的终边经过点P(-3,4),则cosα的值等于()
已知圆M经过A(1,0),B(3,0),C(0,1)三点,则圆M的标准方程为()
已知圆M经过A(1,0),B(3,0),C(0,1)三点,则圆M的标准方程为()
p21蛋白激活的机制是()
已知过点A(1,a),和B(2,4)的直线与直线x−y+1=0垂直,则a的值为( ).
已知过点A(a,2),和B(2,5)的直线与直线x+y+4=0垂直,则a的值为( )
已知过点A(1,a)和B(2,4)的直线与直线x-y+1=0垂直,则a的值为()
已知直线AB及一点P,若过点P作一条直线与AB平行,则这样的直线()
已知角α的终边经过一点P(-3,4),则sinα的值为______
设点P为直线x+y-4=0上的动点,点A(-2,0),B(2,0),则|PA|+|PB|的最小值为()
已知tanα=m(m≠0),则sinα的值是()。
若直线l经过点M(1,1),且与直线x-2y+6=0平行,则直线l的方程为()
已知过点A(a,3),和B(4,5)的直线与直线2x-y+1=0平行,则a的值为( )
已知点P(x,y),且x2+y2=0,则点P在()



 使用微信扫一扫登录
使用微信扫一扫登录